Lehnert, Lucas, et al. "Beyond A*: Better Planning with Transformers via Search Dynamics Bootstrapping." arXiv preprint arXiv:2402.14083 (2024).
The paper being reviewed today suggests a model called Searchformer, which challenges the common belief that Transformers inherently struggle with solving complex decision-making tasks.
TL;DR
Searchformer is a encoder-decoder architecture that is trained to solve complex plannng tasks such as maze and Sokoban. Two variants of models were introduced:
- solution-only model is trained to directly predict the solution from the problem.
- search-augmented model is trained to predict the search dynamics as well as the solution.
The models are trained on the generated datasets of maze and Sokoban puzzle, in which the randomly generated map is marked with $A^\ast$ algorithm-generated optimal solution. However, training a transformer to only mimic $A^\ast$ is impossible to outperform the original algorithm.
Therforer, the authors change the $A^\ast$ algorithm to be non-deterministic and exploit search dynamics bootstrapping to generate solutions with varied sequence length. Among the generated solutions, only the ones that are optimal and has shorter search dynamics are choosed to generate a new dataset. The authors fine-tuned the models on the new dataset, resulting in the final Searchformer model.
Introduction
Suggested in 2017, Transformer architectures have shown remarkable performances in the diverse tasks. However, they still lack the ability to effectively solve planning and reasoning tasks.
Although there are plenty of works that employ neural networks to solve such tasks such as AlphaZero, these works do not exploit the reasoning ability of LLMs but merely use them as function approximators. Another line of works tries to simulate the thinking process of human using Transformers. This includes Chain-of-thoughts(CoT) and Tree-of-thoughts(ToT), but these methods often deteriorates the performance, and have limited range of applicable tasks.
This paper proposes a new way of training Transformer to solve planning and reasoning tasks, using the LLMs capability of reasoning.
The $A^\ast$ algorithm
Searchformer starts off by training the Transformer to imitate $A^\ast$ algorithm, which is an algorithm for computing optimal plan. Let's briefly review how $A^\ast$ algorithm works. Since there are plenty of excellent materials, I recommend referring to those for the readers encountering the $A^\ast$ algorithm for the first time.
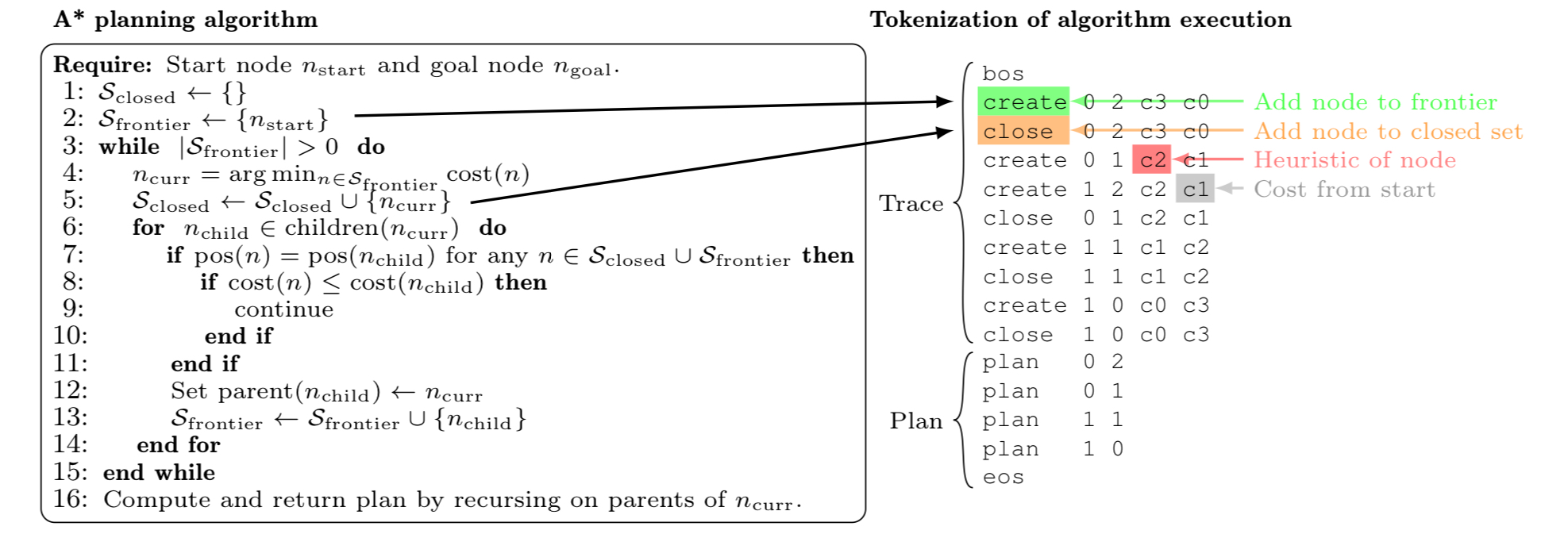
As in the pseudo-code above, $A^\ast$ algorithm uses two sets: $S_{closed}$ and $S_{frontier}$. Here,
- $S_{closed}$ is the set of nodes to which the distance from the start node is already determined.
- $S_{frontier}$ is the working set of nodes where the distance to them are currently being calculated.
This approach, using two sets as above, can also be found in Kruscal's algorithm and Dijkstra's algorithm. However, $A^\ast$ algorithm is different from such algorithms in that it uses a heuristic function to prioritize the search process. While Dijkstra’s algorithm prioritizes the nodes with the least cost of current state $g(x)$, $A^\ast$ algorithm introduces an additional heuristic function $h(x)$ to approximate the expected cost for traversing from the node $x$ to the destination, and use $f(x) = g(x) + h(x)$ as the priority function. In a nutshell,
- Dijkstra’s algorithm fetches the next node $x$ to be searched by choosing the one with minimum cost $g(x)$, which is the cost for traversing from the start node to the node $x$.
- In contrast, the $A^\ast$ algorithm chooses the node with the least $f(x) = g(x) + h(x)$, where
- $h(x)$ is the estimated cost for traversing from node $x$ to the destination node.
Note that $A^\ast$ algorithm is not an approximate algorithm, but is an algorithm that is still guaranteed to find the optimal path as Dijkstra’s algorithm does. The heuristic function just plays the role in reducing the search steps to find the optimal plan. The aim of the paper is not to train Transformer to find a more efficient path(plan), but is to reduce the search steps required to find the optimal path.
When the $A^\ast$ algorithm is run to generate the solutions from the dataset, the execution process is logged into the format demonstrated in the right panel of the above figure. As in the figure, the Trace part encodes the searching process that the $A^\ast$ algorithm undergoes. The Plan part is the resulting optimal plan. Pairing the generated random tasks and the <trace><plan> sequence completes the dataset.
Model Architecture
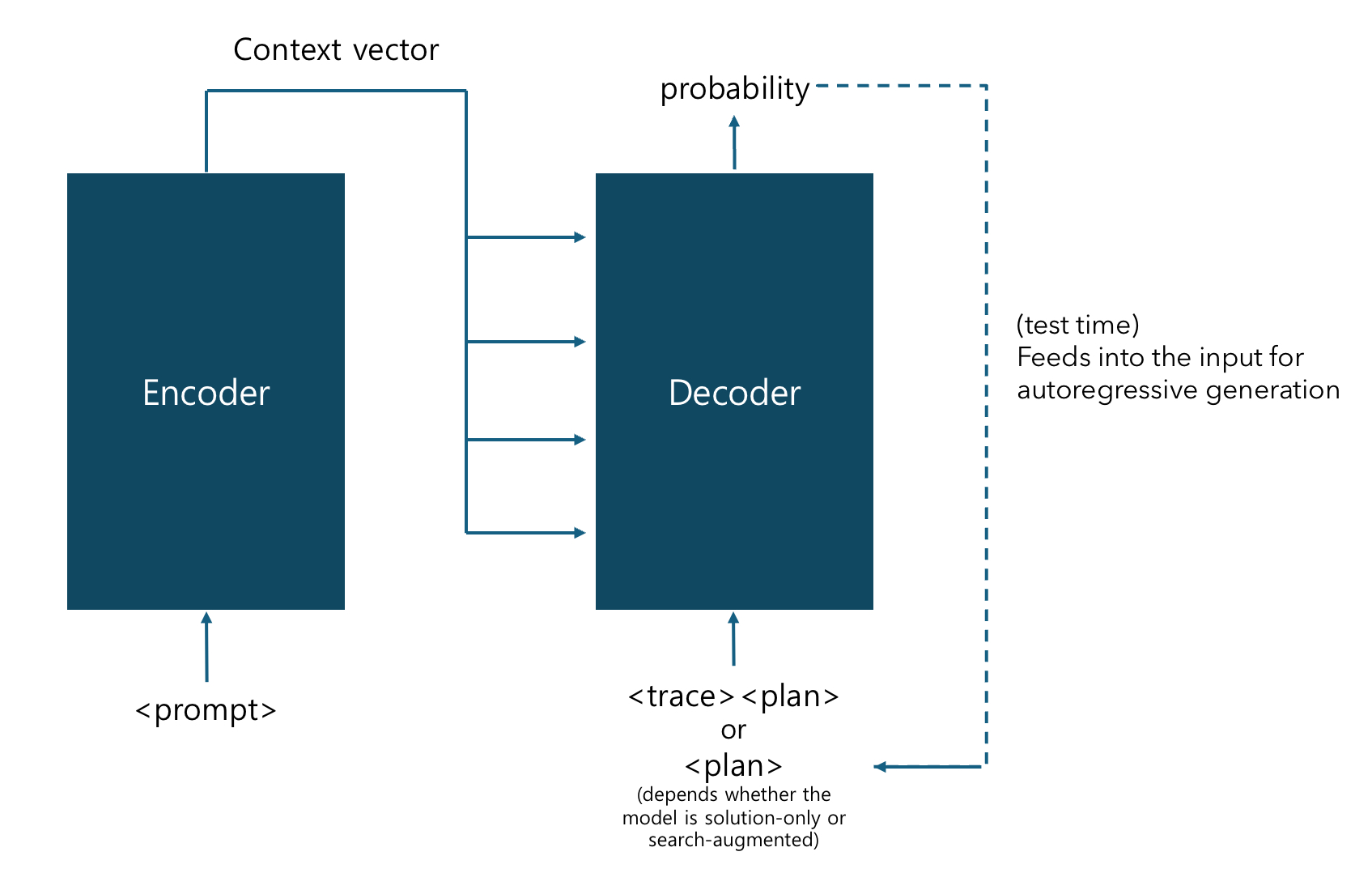
The overall model architecture is demonstrated in the figure above. An encoder-decoder T5 Transformer is introduced and is trained to imitate the $A^\ast$ algorithm. Using the generated dataset tagged with $A^\ast$ solutions, the Transformer is trained either
- to predict only the final solution
<plan> (solution-only model)
- or to predict the tokenized search stage
<trace> as well (search-augmented model)
while the task is formatted as a token sequence to be given as input (<prompt>). Below is an example of a maze task formatted into a token sequence. The coordinates of the start and the goal cell is given after the special tokens start and goal, respectively. The wall cells are also designated in the similar manner. The overall sequence is surrounded by bos and eos tokens (beginning/end of sequence).

Search Dynamics Bootstrapping
Once the training process above is finished, our Transformer model will be able to mimic the A* algorithm in a decent level. But this will not be enough. However high the accuracy is, the transformer is unlikely to outperform the actual $A^\ast$ algorithm. Therefore, there would be no need to use a Transformer, which requires extensive calculation!
This is why the authors further introduces a process named search dynamics bootstrapping. As the preparation step, the authors slightly change the dataset setting. The $A^\ast$ algorithm that was used to generate the labels is modified to be non-deterministic:
- the cost tie breaking is done randomly (first line of the outer loop)
- the child nodes are expanded randomly (the order of iterations of the inner loop)
Training the model on the non-deterministic dataset results in the more varied output of the trained model. Now, the authors feed the entire train dataset into the newly trained non-deterministic Transformer, generating multiple solutions for each of the tasks. Among the resulting sequences, only the solutions that are both
- correct, i. e. the format is right and the path is feasible
- optimal, i. e. the length of the plan is minimal
- and has shorter trace sequence
are selectively collected to construct a new short sequence dataset. The authors fine-tuned the models on the new dataset, resulting in the final Searchformer model. Note that this process can also be repeated. For example, feeding the train set again into the Searchformer and collecting only the short sequences will enable the model to be fine-tuned again to generate shorter traces.
Experiments
Metrics
The results were evaluated with various criteria. Beware that we can classify the generated solutions into three classes:
- an optimal plan,
- a correct but sub-optimal plan,
- or an invalid plan
The evaluation was held both for the maze and Sokoban puzzles. The results are from maze tasks unless mentioned otherwise.
Measuring the plan optimality
The optimality of the output plan was assessed using one of three metrics:
- Exact-match was used to evaluate models trained on the deterministic dataset.
- Any-optimal-64 labels the task correct if at least one of 64 trials generates an optimal plan.
- Success Weighted by Cost(SWC) is a metric calculated by $SWC=\frac{1}{n}\sum\limits_{i=1}^{n}c_i\frac{l_i^\ast}{\text{max}(l_{i},l_i^\ast)}$. For task $i$, outputs are generated 64 times to evaluate SWC. Here, $c_i$ is the any-optimal-64 label, and $t_i$ and $t_i^\ast$ are the search dynamics(trace) length generated by the model and $A^\ast$ algorithm.
Measuring search dynamics length
Followings are the metrics used to assess the search dynamics length.
- Average-on-optimal length calculates the mean search trace length only for the ones that lead to an optimal plan.
- Improved Length Ratio of Search Dyanmics(ILR) score is computed by $ILR=\frac{1}{n} \sum\limits_{i=1}^{n}c_i\frac{t_i^\ast}{t_i}$, where
- $t_i$ and $t_i^\ast$ are the search dynamics length of the model and $A^\ast$
- $c_i$ can be chosen to be either
- the optimality of the solution (ILR-on-optimal)
- the correctness of the solution (ILR-on-correct)
Results
Search-augment vs. Solution-only
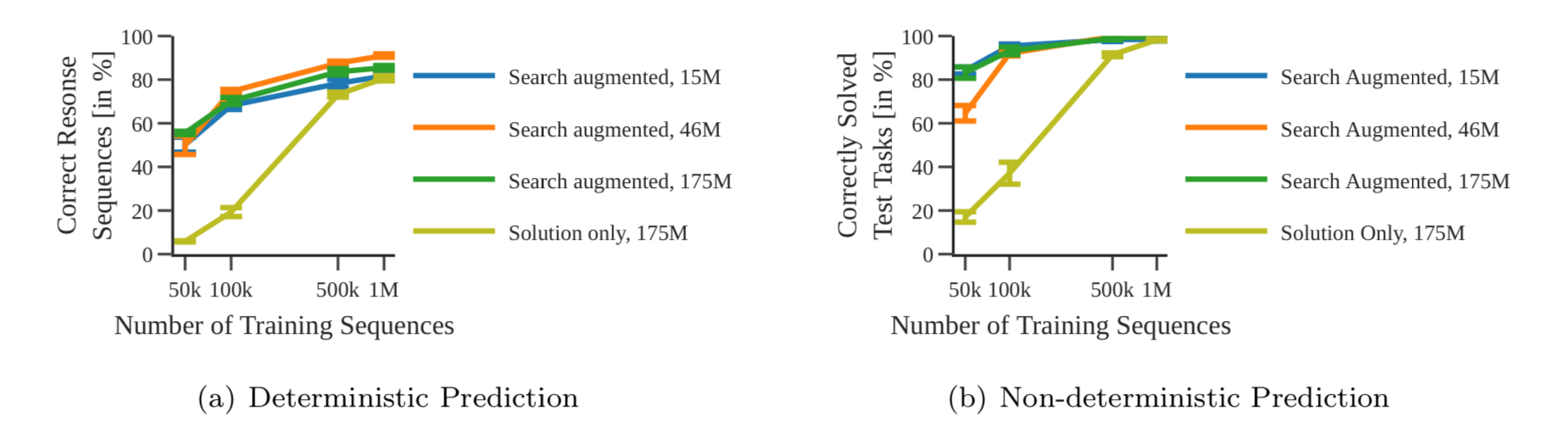
The above figure indicates the portion of correctly solved task for each of the models. As in the both plots, even the smallest search-augmented model outperformed the largest solution-only model. This is a surprising result considering that search-augmented models have output lengths 10+ times larger than solution-only models. Also, the figures indicate that model size impacts the performance only when the dataset is small.
Search-augmented models can be thought of as benefited from generating the search trace. When the model generates the next token auto-regressively, the model refers to the input prompt as well as the already generated search trace sequence. This is similar to the logical thinking process of human, contemplating the next branch to search.
In contrast, solution-only models are trained to find the direct correlation between the input prompt and the solution plan. Many of these correlations may turn out to be fake in test time, especially when the dataset is small.
Effect of Iterative Bootstrapping
As previously mentioned, the bootstrapping can be held repeatedly to further improve the performance. The authors also have studied if the iterative bootstrapping actually reduces the number of search steps.
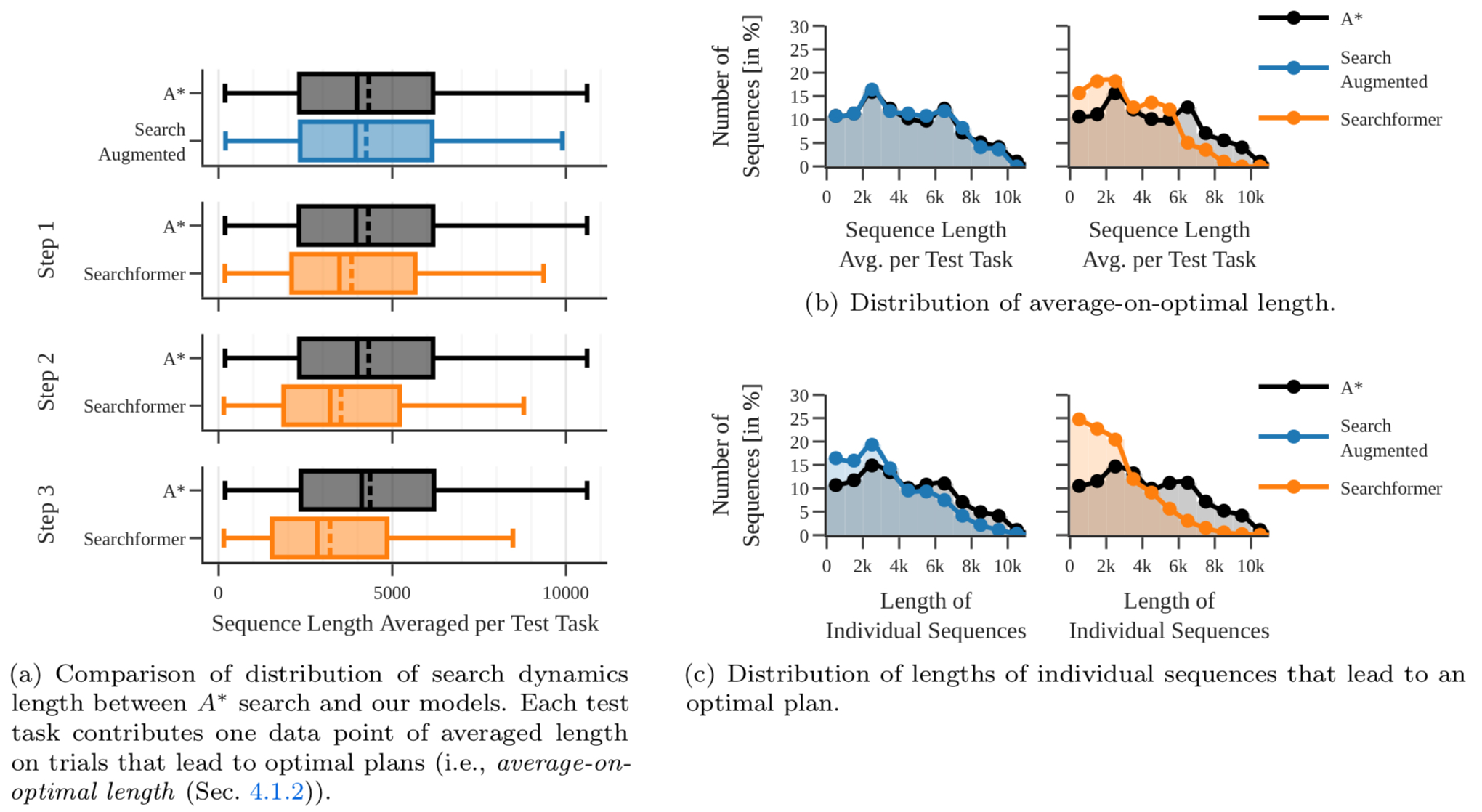
As in the subfigure (a) in the above figure, the sequence lengths were significantly reduced as the bootstrapping was repeated. Subfigures (b) and (c) demonstrates the overall distribution of sequence length also significantly shifts to the left, compared to the base Search-Augmented model where bootstrapping was not applied.
Sokoban Results
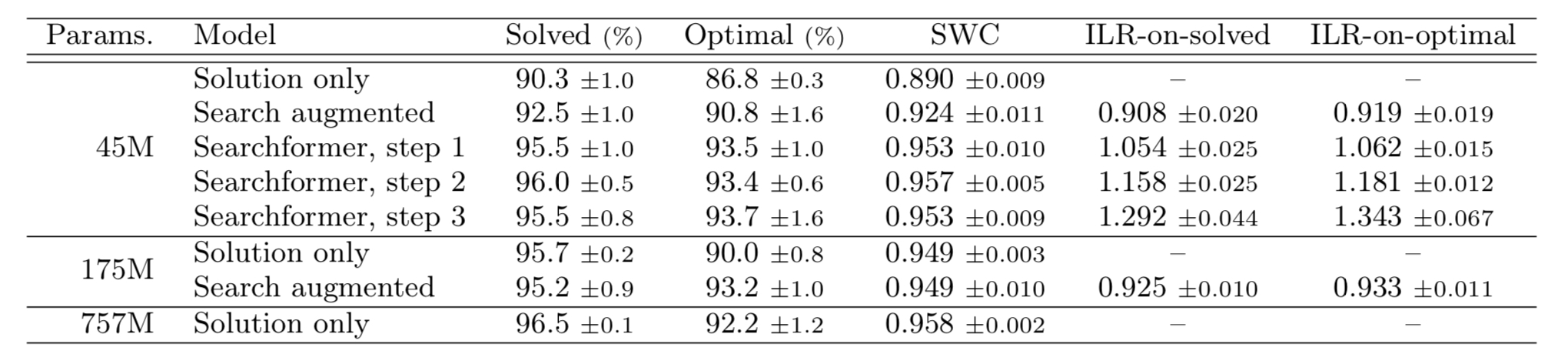
The above table demonstrates the performance of Searchformer on Sokoban puzzles. Searchformers succeeded to solve the puzzles with above 95% chance, and were also able to come up with the optimal solution. Sokoban results also indicate that repeatedly held fine-tuning(bootstrapping) improved the portion of solved and optimally solved tasks, supporting the findings from the maze tasks.