ZeRO: Zero Redundancy Optimization

Rajbhandari, Samyam, et al. "Zero: Memory optimizations toward training trillion parameter models." SC20: International Conference for High Performance Computing, Networking, Storage and Analysis. IEEE, 2020.

Abstract

One of the fundamental limitations in training a large neural network is the GPU memory occupation. To handle this problem, there are a bunch of existing solutions that exploit parallelism to reduce the per-device memory consumption. However, even these solutions do not reduce the memory footprint linearly by the number of devices, due to several overheads.

The authors suggests ZeRO, Zero Redundancy Optimization, as a solution that optimizes the memory consumption, increases training speed, and enlarges the model size that is effectively trainable. ZeRO eliminates the redundancies of memory consumption in the previous methods, while retaining low communication volume. As a result, ZeRO allows the neural network models to be scaled up proportional to the number of devices. ZeRo is implemented and evaluated to train large model which has the unprecedented number of parameters, and achieves the SOTA accuracy.

Background

As deep neural networks began to have increasingly large number of parameters, the memory requirement to train these models have become more and more demanding. For example, to train GPT-2, which has 1.5 billion parameters, the device to train it must have more than 24GB of memory.

To cope with this problem, numerous solutions were proposed to parallelize the training process.

• Data Parallelism (DP) is a solution that can be employed when the model size fits into a single device. When DP is exploited, a number of GPUs undergo forward/backward propagation with the same model, using different input datas. Once each device gets the gradient based on its own data, the gradients are gathered and averaged to update the shared parameters.

As opposed to DP, there also are the techniques that can be applied even when model size is too large to be trained in a single GPU.

• Model Parallelism (MP), in contrast, slices the model vertically. Therefore, parameters of the same layer can be split to be loaded to different devices.
• Pipeline Parallelism (PP) slices the model horizontally, e. g. first few layers are loaded to device 0, whereas the next few layers to device 1, and so on.

Analysis of Memory Consumption

To overcome the limitations of existing solutions, the authors first analyze the components of train-time memory footprint and classify into two parts: model states and residual states.

Model states comprises the memory occupied by the model (1) parameters, (2) their gradients, and (3) the optimizer states. Among these, most of the memory footprint comes from optimizers. This is because modern optimizers, e.g., Adam, store other information such as the running average and the variance of the gradients. The authors epitomizes Adam with mixed-precision applied as the target of analysis. This case, assuming the parameter number $\Psi$,

• Parameters are stored in FP16 and occupy $2\Psi$ bytes
• Their gradients, which are also stored in FP16, occupy another $2\Psi$ bytes
• The optimizer states possess $12\Psi$ bytes of memory footprint, since
  • they keep the FP32 copy of the parameters, ($4\Psi$ byte)
  • the momentum (running average) of the gradient, ($4\Psi$ byte)
  • and the variance of gradient ($4\Psi$ byte)

Dubbing the memory multiplier of optimizer as $K$, we draw the conclusion that total of $(2+2+K)\Psi=16\Psi$ bytes of memory is required to train a model with $\Psi$ parameters.

Residual states refer to the remaining memory footprint. This includes the (1) activation, (2) temporary buffers and (3) unusable fragmented memory.

• Activations take a significant amount of memory. To reduce this, activation checkpointing (a.k.a. gradient checkpointing) is often applied to save only the $\sqrt{n}$-th activations with expense of 33% increase in computation overhead. ¹ However, for larger models, activation memory can be still significantly large even after the activation checkpointing.
• Temporary buffers are used to store intermediate results that are used for operations such as gradient all-reduce, or gradient norm computation. These operations gather all the gradients into a single temporary buffer before the operations are actually applied, resulting in the redundant memory footprint of the buffer.
• Memory fragmentation reduces the available memory size, even if there actually are free memory spaces. The impact of the phenomenon to the memory footprint is more significant, especially when we train a very large model.

The authors devise a solution, ZeRO, to reduce the redundant memory caused by each of the components introduced.

ZeRO-DP: Optimize Model State Memory

The authors first suggest ZeRO-DP, which reduces the model state memory. To do so, the authors studied the pros and cons of DP and MP as follows:

Method	Pros	Cons	Shared Aspects
DP	Good computation efficiency due to larger computational granularity. Less communication volume (= Good communication efficiency).	Poor memory efficiency since it replicates the entire model across all the parallel processes.	Maintain all the model states, even though not all of them are required all the time during the training
MP	Good memory efficiency, since it partitions the model parameters instead of replicating them	Poor computation, since the operations become too fine-grained. Poor communication efficiency.

Based on these observations, the authors come up with an algorithm called ZeRO-DP. Instead of replicating the entire model parameters (as DP does), ZeRO-DP partitions the model state, a la MP. ZeRO-DP also employs dynamic communication scheduling to optimize the communication volume. As a result, ZeRO-DP achieves both the computation/communication efficiency of DP and the memory efficiency of MP.

Since the model state comprises three components — optimizer, gradient, and parameter, ZeRO-DP includes three techniques that optimizes the memory use of each. The techniques are applied cumulatively in the following order.

1. Optimizer State Partition ($P_{os}$): 4x memory reduction, while maintaining same communication volume as DP.
2. Gradient Partitioning ($P_{os+g}$): 8x memory reduction, same communication volume.
3. Parameter Partitioning ($P_{os+g+p}$): Memory reduction proportional to DP degree $N_d$, 50% increase in communication volume.

Let’s take a deeper look into each. Keep in mind that ZeRO-DP is basically a DP strategy. Thus, the data treated in each process are all different.

$P_{os}$: Optimizer State Partitioning

Firstly, the optimizer state is partitioned $N_d$-fold. With $P_{os}$ applied, the $i$-th GPU will be possessing the $i$-th partition of the optimizer state. This does not impact the forward and backward propagation at all. The only component that is affected comes at the end of each training step. When there is the need to update the parameters, the optimizer states are gathered together via all-gather operation.²

As the result of $P_{os}$, the model state memory is reduced from $16\Psi$ to $4\Psi+\frac{12}{N_d}\Psi$. When $N_d$ is large enough, we achieve approximately 4x memory reduction.

$P_g$: Gradient Partitioning

After $P_{os}$ is applied, each process will be updating only the portion of parameter it is in charge of. Therefore, we can also partition the gradients so that each process keeps only the gradients corresponding to their own split of parameters. This is accomplished by reduce-scatter operation. After the gradients are obtained in each of the parallel processes, they have to be reduced to compute the average value, followed by the splitting process that distributes the averaged gradients to each process.

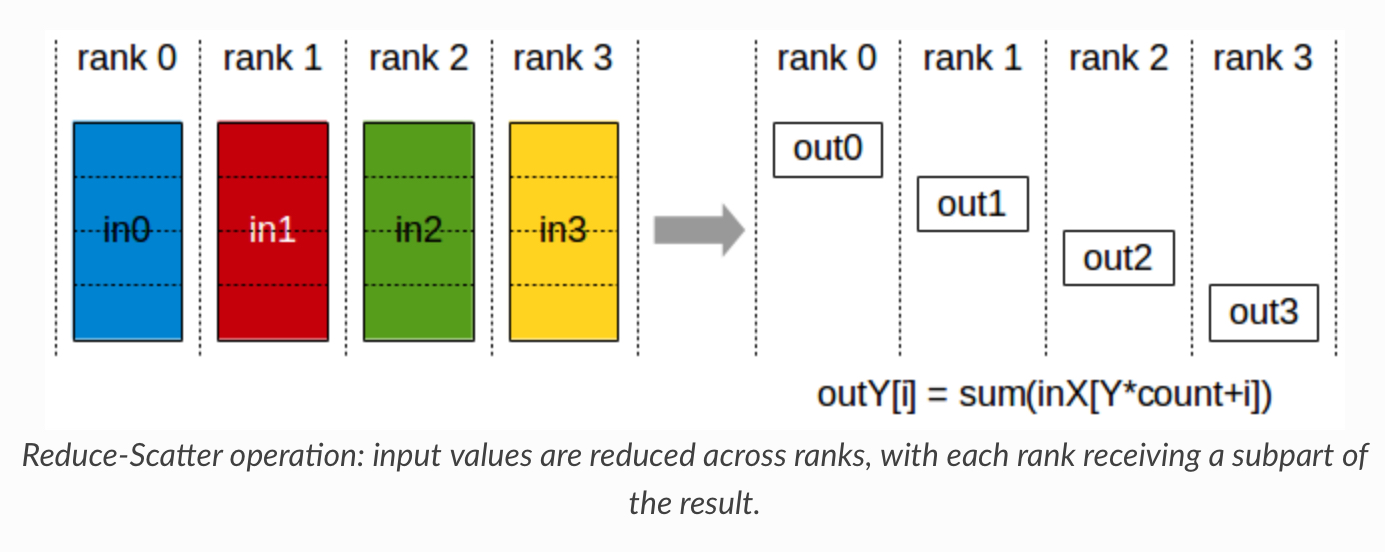
This further reduces the model state memory from $4\Psi+\frac{12}{Nd}\Psi$ to $2\Psi+\frac{14}{Nd}\Psi\approx 2\Psi$.

$P_{p}$: Parameter Partitioning

The ultimate optimization step of ZeRO-DP is to partition the parameters themselves across the parallel processes. During the forward/backward pass, each process receives the required parameter split from other processes on-demand. As the final result, the memory footprint is reduced to $\frac{16}{N_{d}}\Psi$. This implies you can train a model with an arbitrary size as long as you have sufficiently many GPUs!

ZeRO-R: Optimize Residual State Memory

As introduced previously, the residual state of a network while training consists of three components: activations, temporary buffer, and fragmented memory. This is where ZeRO-R comes into the play, to handle the memory inefficiencies of each.

1. Activation memory is reduced by identifying and removing activation replications in the existing MP approach.
2. Temporary buffers are fixed in size, to avoid them from growing up as models enlarge.
3. Fragmented memory arises due to varying lifetime of tensors stored in contiguous locations. For example, among the activations during the forward pass, those that are checkpointed are long-lived, whereas those that are not are short-lived. On par, during the backward pass, activation gradients are short-lived whereas parameter gradients are long-lived.

Let’s go through the details of each.

$P_a$: Partitioned Activation Checkpointing

Even though MP partitions the model states, they often replicate the activation memory. For example, assume a layer vertically split across two GPUs. For the input to be fed into the both halves, it must be replicated and stored in the both devices in prior.

To cope with this inefficiency, ZeRO-R applies two techniques. First, it applies activation checkpointing, reducing the number of activations that are stored in the memory all the time. Secondly, ZeRO-R further partitions the checkpointed activations across the GPUs. When it faces the need to reconstruct the activations, whether during the forward or backward propagation, it exploits all-gather operation to reconstruct them on demand. Through this, the memory occupied by activations are reduced significantly.

However, the authors were not satisfied even at this point. In the case of training a very large model, the partitioned checkpoints are offloaded to CPU memory, which the authors refer to as $P_{a+cpu}$. With this technique applied, the memory footprint due to activation becomes near zero.

$C_B$: Constant Size Buffer

ZeRO fixes the size of the temporary buffer, to prevent it from becoming too memory-consuming when the model has a large size.

$M_D$: Memory Defragmentation

Fragmented memory poses two problems:

• It may cause OOM(out-of-memory) even when there actually are (fragmented) free memory spaces.
• It impacts the performance, since it makes the memory allocator take a significant time searching for free space.

To cope with these problems, ZeRO pre-allocates contiguous memory chunks for the gradient and the parameter checkpoints. When there arises a need for allocating a new memory, the pre-allocated memory is utilized. This not only increases the size of available memory, but also improves the performance.

ZeRO-DP and ZeRO-R combined together forms the powerful optimization solution, which the authors refer to as ZeRO.

Communication Analyses

This chapter analyzes the impact of ZeRO-DP and ZeRO-R to the communication volume. Starting from the conclusion,

• Only $P_p$ affects the communication volume among the techniques of ZeRO-DP. Even when $P_p$ is introduced, the communication volume increases by maximum of 50%.
• Among the optimizations in ZeRO-R, only $P_a$ impacts the communication volume and enlarges it by less than 10%.

Communication Analysis of ZeRO-DP

DP Communication Volume
To set the baseline, let's go through the communication volume caused by standard DP first. At the end of each step during the data parallel training, the gradients computed by each process with different data points must be averaged to update the parameters. This is essentially an all-reduce operation, which is implemented in two steps: (1) reduce- scatter and (2) all-gather. The computation steps can be demonstrated as follows:

• Initially, the $i$-th process has the gradient $\nabla L_i$ ($L_i$: loss calculated from $i$-th data).
• As the result of reduce-scatter, the split version of averaged gradient $\nabla L = \frac{1}{N}(\nabla L_1 + \cdots \nabla L_{N_d})$ are distributed to each process.
• After all-gather operation is held, all the process will be given the whole gradient $\nabla L$ .

Since each step costs $\Psi$ bytes, the standard DP process incurs total of $2\Psi$ bytes of communication volume per process.

ZeRO-DP Communication Volume
Now, let’s calculate the communication volume when ZeRO-DP is applied. Firstly, ZeRO-DP does not require any additional communication when $P_{os}$ or $P_{os+g}$ is introduced. In these cases, each device only stores the part of gradients that corresponds to their share of parameters. Therefore, instead of all-reduce, ZeRO-DP only requires the reduce-scatter operation to the gradients, which takes $\Psi$ bytes of communication per device.

After each device updates their portion of parameters (using the reduce-scattered gradients), it needs to share their share of updated parameters with other processes. This requires another communication volume of $\Psi$, resulting in the total volume of $2\Psi$. This is the same amount with that required by standard DP.

What about when $P_{os+g+p}$ is applied? This case, the processes need to collect the portions of parameters that they do not possess to do forward pass. However, they do not gather all the parameters at once, but pipeline them instead. For example, it gets the $\theta_1$, does the forward pass to get the first activation, and discards $\theta_1$. After that, it collects the next parameter partition, $\theta_2$, computes the next activation, discards $\theta_2$, and so on. ³ This costs the total communication volume of $\Psi$.

This forward propagation process needs to be held twice: once during the forward propagation, and again to recompute the activations during the backprop. In addition, the resultant gradients must be reduce-scattered, resulting in the communication volume of $3\Psi$. This is 50% increase from the original DP.

Communication Analysis of ZeRO-R

Then how does ZeRO-R impact the communication? ZeRO-R increases the communication volume by less than 10%, as explained below. Standard MP, for example, that used in Megatron-LM, requires total of six all-reduce operation: twice for forward pass, twice more for forward recomputation during backprop and another twice for backward propagation. ZeRO-R, in the same sense, requires all of the all-reduce operations in standard MP. In addition, since it partitions the activation checkpoints, an all-gather operation must be introduced before the forward recomputation during backward pass. This causes about 10% of communication overhead.

When MP is jointly applied with DP, $P_a$ can come into the play and reduce the data-parallel communication by an order of magnitude, by trading only 10% increase in communication. This is because MP allows a larger batch size, which results in the reduction in the number of batches. This means the model undergoes less number of training steps, which reduces the data-parallel communication volume.

Implementation and Evaluation

The authors suggests the possibility of training a trillion-parameter model when powered by ZeRO, which is three orders of magnitude larger than the SOTA model when the paper was published. As a demonstration, they trained the model that has the unprecedentedly large number of parameters, namely, ZeRO-100B. During training, authors observed super-linear scalability for very large model size. That is, the performance increased more than linearly with the number of GPUs. This is considered to be the result of the reduction in the communication volume when the degree of parallelism is increased.

Conclusion

One of the biggest obstacles in scaling neural models is the lack of sufficient memory to train them. There are many solutions to parallelize the training process, but per-device memory footprint were not reduced inversely proportional with the number of devices ($N_d$).

ZeRO provides a new landscape in large model training. As opposed to existing training parallelism methods, ZeRO reduces the per-device memory footprint by the denominator of $N_d$. This enables the training of arbitrarily large models, as long as there are enough number of available devices.

ZeRO is available as the part of DeepSpeed library. By using it, researchers can easily introduce the optimizations in ZeRO, simply without the need of refactoring the model.