
Lewis, Patrick, et al. "Retrieval-augmented generation for knowledge-intensive nlp tasks." Advances in Neural Information Processing Systems 33 (2020): 9459-9474.
TL;DR
LLMs can store enormous amount of knowledge implicitly inside its parameters. However, it is impossible to manipulate or access the knowledge contained in the parameter, which makes LLMs inferior to task-specific architectures in the knowledge-intensive tasks. Also, they struggle with updating the stored knowledge or providing the evidence of its knowledge.
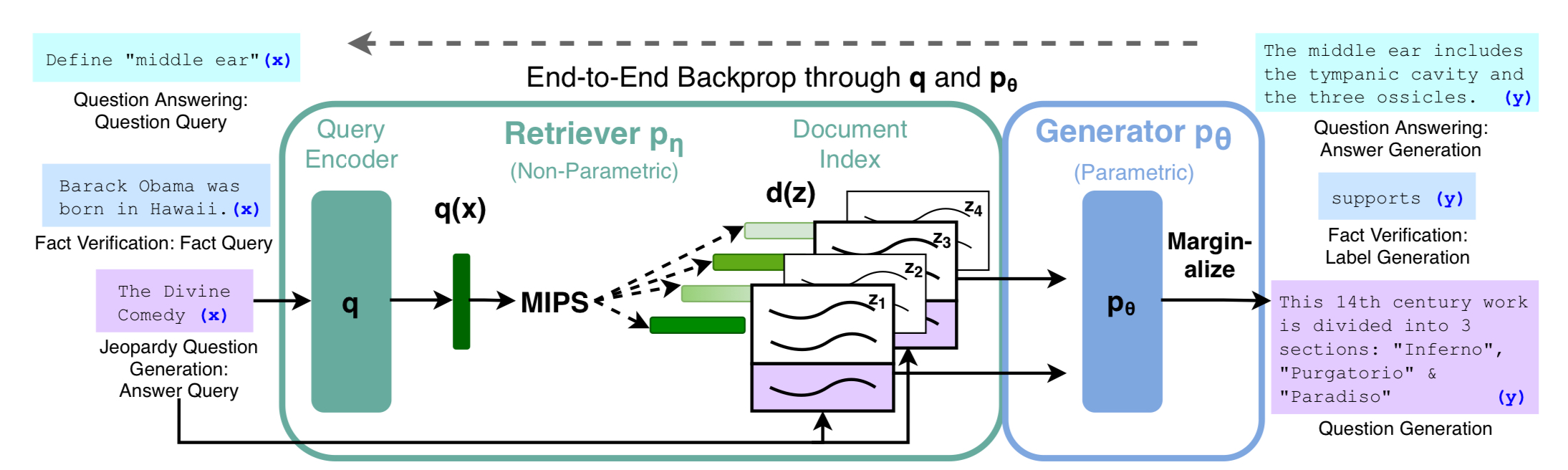
The Retrieval-Augmented Generation (RAG) is the model that augments the parametric memory(i. e., the parameters of a seq2seq model) with nonparametric memory, which is dense vector index of Wikipedia. The retriever model fetches the relevant information from the nonparametric memory, and this is fed into the seq2seq model to be exploited to generate text.
The paper suggests two formulations of RAG: (1) one that references a single document in the entire generation process, and (2) the other that uses different documents in the per-token basis. As a result of the fine-tuning using these two models, the authors have achieved the SOTA or near-SOTA performances from several knowledge-intensive NLP benchmarks.
Augment LLMs with Non-parametrized Memory
Pre-trained LLMs save enormous amount of knowledge implicitly inside its parameters. Nevertheless, due to their implicit nature, it is difficult to modify the content or track the source of their knowledge. Also, the problem of hallucination arises.
RAG (Retrieval-Augmented Generation) is a hybrid model that augment retrieval-based, non-parametrized memory to LLMs to cope with these problems. As opposed to the existing hybrid models that were applicable only to extractive questions answering, RAG employs seq2seq to generate the answer based on the input query and the fetched document. Here,
- seq2seq transformer performs as a parametric memory, which stores the information implicitly in its parameter. This is called the generator part of RAG architecture, since it also plays the role of generating the output text.
- the Wikipedia was used as the nonparametric counterpart. This is where Dense Parametric Retriever (DPR) comes into the play, which retrieves K most relevant documents based on the input query.
RAG is composed up with two components:
- the retriever $p_\eta(z|x)$ returns the (top-K truncated) distribution of text passages $z$, given the query text $x$.
- the generator $p_\theta(y_i| x, z, y_{1:i-1})$ generates the current token $y_i$ based on the previously generated tokens $y_{1:i-1})$, the query text $x$, and the retrieved passage $z$.
The authors suggest two formulations for RAG:
- RAG-Sequence uses the same document to predict each target of the output sequence.
- RAG-Token uses different passages to generate each token.
Let’s take a deeper look into each formulation mathematically.
RAG-Sequence
RAG-Sequence first computes the top K most relevant documents, based on the input sequence. After that, each of the K documents is used to generate the entire target sequence, followed by the generator probability being marginalized against the documents:
$$p_{RAG-Sequence}(y|x) \approx \sum\limits_{z\in\text{top-k}(p(\cdot|x))} p_\eta(z|x) p_\theta(y|x, z)$$
$$=\sum\limits_{z\in\text{top-k}(p(\cdot|x))} p_\eta(z|x) \prod\limits_i^N p_\theta(y_i|x, z, y_{1:i-1})$$
RAG-Token
As opposed to RAG-Sequence, RAG-Token takes into all of the K retrieved documents to generate each of the tokens in the target sequence. More rigorously speaking, the generator produces a distribution of next token for each document before it marginalizes against the document distribution:
$$p_{RAG-Token}(y|x) = \prod\limits_i^N p(y_i|y_{1:i-1}, x)$$
$$\approx \prod\limits_i^N \sum\limits_{z\in\text{top-k}(p(\cdot|x))} p_\eta (z|x)p_\theta (y_i|x, z_i, y_{1:i-1})$$
The Architecture: Retriever & Generator
Retriever: Dense Passage Retriever
The retriever component is based on DPR (Dense Passage Retriever), here, the word “dense” means it uses a langauge model to encode each document to a latent vector. Conversely, sparse retrievers use methods such as TF-IDF to map the documents to vector space.
Here, the DPR exploits a bi-encoder architecture, that is, it uses two BERT-base LMs to encode the documents and the input query, respectively. The document with the greatest inner product with the input query is considered as most relevant. Mathematically,
$$p_\eta(z|x) \sim \exp(\mathbf{d}(z)^T \mathbf{q}(z))$$
where $\mathbf{d}(z)$ and $\mathbf{q}(z)$ are the latent vectors for the document and the query, respectively. This is a Maximum Inner Product Search (MIPS) problem, which is known to have a sub-linear solution.
Among the two BERT models, only the one for input prompt ($\mathbf{q}(z)$) was fine-tuned, freezing the parameters of $\mathbf{d}(z)$. The set of vector indices is what the authors refer to as the non-parametric memory.
Generator: BART
For the generator counterpart, the language model BART-large is exploited to generate the output text based on the retrieved documents and the prompt. To feed the inputs into the language model, the retrieved content $z$ and the input prompt $x$ are simply concatenated. The parameters of BART model is what the authors refer to as the parametric memory of RAG. The retriever and the generator were jointly trained end-to-end to minimize the loss function $\sum_j -\log p(y_j|x_j)$, given the fine-tuning corpus of pairs $(x_j, y_j)$. Before the training, all of the models were initialized with pretrained parameters.
Decoding
At the test time, the two formulations of RAG have to undergo the different decoding process.
RAG-Token
Since the probability formula for RAG-Token matches with standard autoregressive seq2seq models, the standard beam decoding with transition probability $p_\theta’(y_i|x_i, y_{1:i-1}) = \sum\limits_{z\in\text{top-k}(p(\cdot|x))} p_\eta (z|x)p_\theta (y_i|x, z_i, y_{1:i-1})$ plugged in can be used. Note that the transition probability here is identical to the formula for $p(y|x)$, with only the $\prod_i$ is excluded.
RAG-Sequence
However, the formula for RAG-Sequence cannot be split into conventional token likelihood, making the traditional beam search impossible. This is because RAG-Sequence generates the whole sentence at once for each of the retrieved passages. Instead, the decoder runs the beam search for each of the retrieved documents $z$, using transition probability $p_\theta(y_i|x, z, y_{1:i-1}$. As a result, each document is matches with a number of target sentence candidates.
To calculate the final probability of target sequences $y$, the decoder has to calculate $p(y) = \sum_z p(y|z)p(z|x)$. However, the value of $p(y|z)$ cannot be directly evaluated if the target sequence $y$ has not appeared during the beam search using $z$. As a solution, The authors propose two strategies for decoding:
- Thorough Decoding runs an additional forward pass to calculate $p(y|z)$, using teacher forcing.
- Fast Decoding neglects $p(y|z)$ to be 0, when $y$ did not appear.
Experiments
Tasks
Four tasks were introduced to assess the performance of RAG.
- Open-domain Question Answering
- Abstractive Question Answering, in which the model would be impossible to answer the question using its inherent knowledge without accessing the “gold passage”.
- e. g. “What is the weather in Volcano, CA?”
- Jeopardy Question Generation, in which the model has to generate “Jeopardy” questions, which is the questions guessing the subject based on the given fact about the subject.
- e.g. “In 1986, Mexico scored as the first country to host this international sports competition twice.” is a Jeopardy question with answer “The World Cup.”
- Fact Verification, which is the task determining if the given statement is either {supported, refuted}, or {supported, refuted, unverifiable} based on the Wikipedia.
Results
Open-Domaian and Abstractive Question Answering
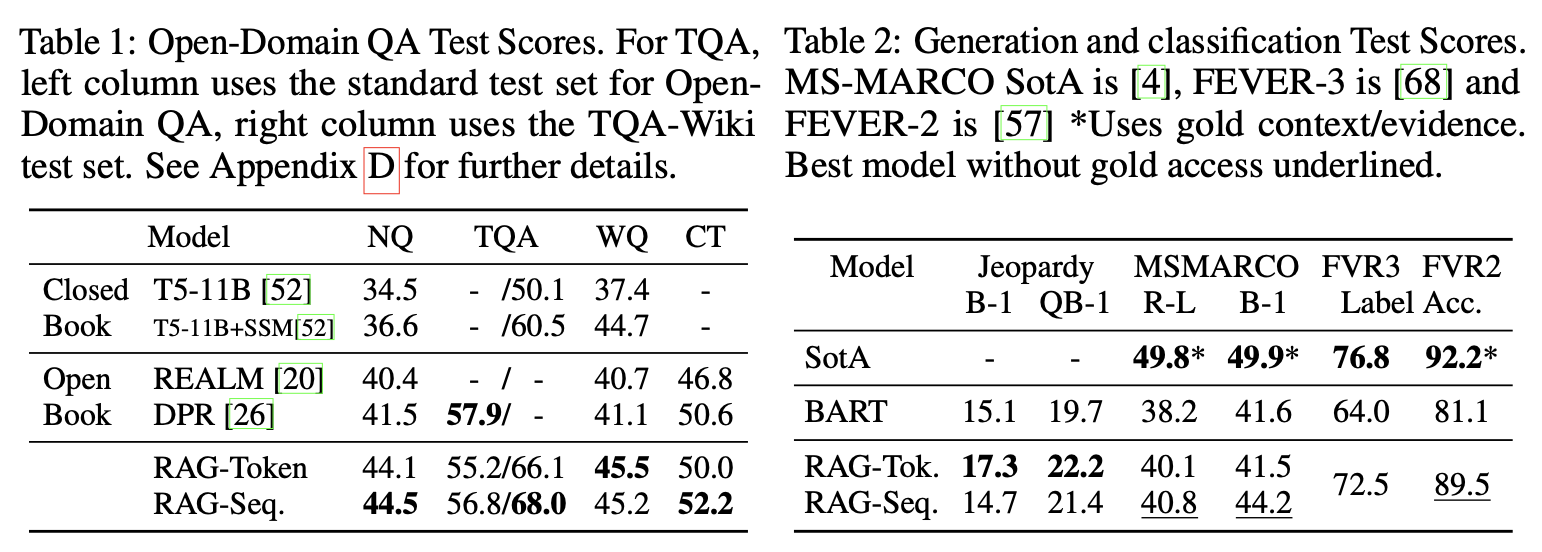
As shown in Table 1, RAG achieved SOTA or near-SOTA performances on Open Domain QA datasets. It also outperformed BART on Open MS-MARCO NLG dataset for abstractive question answering (Table 2). This indicates that RAG has the ability to identify the gold passage needed to answer the question.
Jeopardy Question Generation
In the jeopardy question generation task, RAG also outperformed BART (Table 2). Among the two variants, RAG-Token was shown to have performed better than RAG-Sequence. This is due to its nature generating the sequence based on the information of multiple documents combined.

Above is the plot of posterior $p(z_i|x, y_j)$ when the model generates the title of a book "A Farewell to Arms." High value of posterior indicates that the model depended heavily on the document during the generation. The figure indicates that RAG depends on the non-parametric knowledge only at the beginning of the sentence, while the consecutive tokens were generated based on the generator's own abilty of language modelling. Thus, the role of non-parametric knowledge can be considered as to elicit the knowledge that is already existent in the parametric memory.
Fact Verification
RAG showed a remarkable performance in fact verification, although it did not beat SotA model which has very complicated and domain-specific architecture (Table 2). Also, the authors could discover that the top retrieved document was from the gold article in 71% of the cases, and the gold article was in the top 10 relevant document in 90% of the cases.
Additional Result
- The authors measured the generation diversity by calculating the ratio of distinct n-grams over the total n-grams. As a result, RAG-Sequence was shown to be generating more diversified sequence, where both models' generations were significantly more diverse than that of BART.
- Retrieval Ablations: The authors replaced the retriever to be (1) unchanged (2) same, but unlearnable (3) word overlap based BM25 retriever. The results showed that BM25 performs better only on FEVER task, where the incumbent retriever won in every other tasks.
- Index hot-swapping: The authors replaced the dense vector index into that of 2016 and 2018, and asked the questions about the world leaders as of both dates. The model succeeded to guess the leader with ~70% chance when the dates coincided, but did so with 12% and 4% chance when the dates were different.