Dao, Tri, et al. "Flashattention: Fast and memory-efficient exact attention with io-awareness." Advances in Neural Information Processing Systems 35 (2022): 16344-16359.
IO를 고려해 어텐션 메커니즘을 효율적으로 구현한 FlashAttention 논문을 정리해본다.
Abstract
트랜스포머는 시퀀스 길이의 제곱에 비례하는 시간/공간 복잡도를 갖는다. 이를 해결하기 계산의 복잡도를 낮춘 근사 어텐션 알고리즘들이 있으나, 많은 경우 실제 속도 향상 폭은 크지 않았다.
이 논문에서는 어텐션을 IO-aware하게 만드는 것이(i.e. GPU 메모리의 각 단계 사이의 읽기/쓰기를 최소화 하는 것이) 트랜스포머 속도 향상을 위한 해결책임을 주장하고, 이를 적용한 FlashAttention 아키텍처를 제안한다. FlashAttention은 (근사법이 아닌) 어텐션을 정확하게 계산하는 알고리즘이면서도 그 어떠한 근사 어텐션 알고리즘보다 빠르게 작동한다는 점에서 시사하는 바가 크다.
1. Introduction
트랜스포머는 시퀀스 길이의 제곱에 비례하는 시간/공간 복잡도를 가져 이해 가능한 context의 길이를 길게 만드는 것이 어렵다. 이를 해결하기 위해 복잡도를 O(n)으로 줄인 approximate attention method들이 제안되었으나 실제 계산 속도에 유의미한 향상을 보여주지는 못했다.
저자들은 이러한 approximate method들이 실패한 이유가 FLOPS 수를 감소시키는 데에만 초점을 맞추고, 메모리 접근에 의한 오버헤드에는 관심을 기울이지 않았기 때문이라고 주장한다. 현대 GPU에서 transformer에 해당하는 계산을 할 때, 대부분의 bottleneck은 메모리에서 발생하기 때문이다.
논문은 transformer를 IO-aware하게 만들어 작고 빠른 on-chip SRAM과 크고 느린 GPU High Bandwidth Memory (HBM) 사이의 읽기/쓰기 횟수를 최소화하는 것을 목표로 한다. 이것을 위해서 두 군데의 bottleneck을 공략한다:
- softmax 계산 시에 전체 데이터에 접근하지 않아도 되도록 한다.
- backward pass를 위해 중간계산 결과로 나오는 attention matrix를 저장해두는 과정을 없앤다. (일반적으로는 이를 backward pass시 HBM에서 읽어온다)
논문은 이러한 목표를 달성하기 위해 잘 알려진 두 테크닉을 적용한다.
- Tiling: 입력 행렬을 블럭들로 쪼개어, 이를 기본 단위로 하여 incremental하게 계산을 수행한다.
- Recomputation: forward pass에서 계산된 softmax의 분모를 저장해두었다가, backward pass시에 on-chip에서 계산에 사용할 수 있게 한다.
이렇게 attention 계산을 구현하는 새로운 알고리즘을 저자들은 FlashAttention이라 이름붙이고, CUDA를 이용해 구현하였다. 실험 결과에 따르면, FlashAttention은 표준적인 구현에 비해서 FLOPs 수가 더 높지만 더 빨리 실행되고(GPT-2에서 최대 7.6배), 메모리 사용량이 입력 sequence 길이에 선형으로 비례하여 더 적은 메모리를 사용한다고 한다.
저자들은 이후의 챕터들에서 FlashAttention의 IO complexity를 분석하고, attention을 (근사하지 않고) 정확하게 계산하는 알고리즘은 점근적으로 FlashAttention보다 IO complexity가 더 낮을 수 없음을 증명한다. 또한, FlashAttention을 응용하여 approximate attention algorithm인 block-sparse FlashAttention을 제안하고 성능을 비교한다.
2. Background
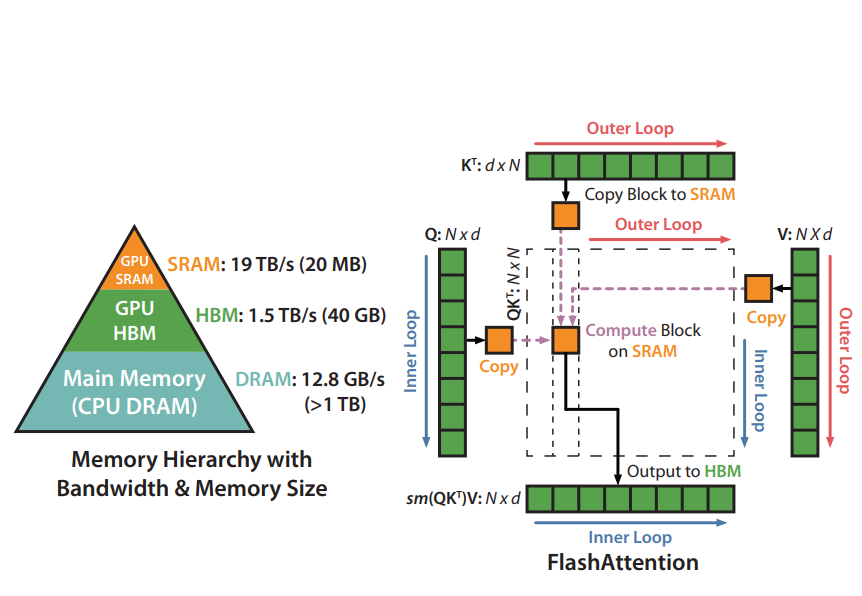
GPU의 메모리는 아래 그림과 같이 hierarchy를 가지고 구성되어 있다.
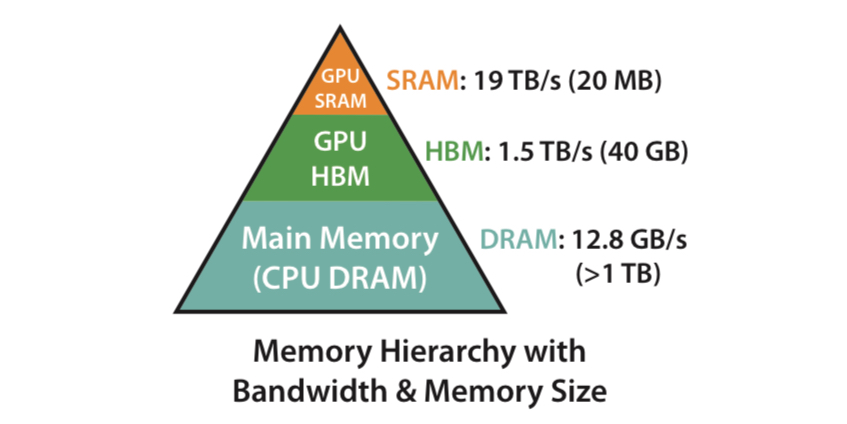
일반적으로 가장 빠르지만 용량이 작은 on-chip SRAM이 있으며, 그 아래 단계로 GPU High Bandwidth Memory(HBM)과 CPU의 메인 메모리가 있는 형태이다. GPU는 계산을 할 때
- HBM(global memory 등)에서 SRAM(shared memory)으로 데이터를 로드하고
- GPU가 SRAM에 데이터를 놓고 계산한 후
- 계산 결과를 HBM에 저장하는 execution model을 따른다.
이 중 병목이 어디에 존재하는지에 따라 GPU의 연산을 두 가지로 나눌 수 있다.
- compute-bound한 연산들은 실제 arithmetic operation들이 병목으로 작용하는 연산들이다. 예시로는 inner dimension이 클 때의 행렬 곱셈이나 채널 수가 많은 컨볼루션 연산이 있다.
- memory-bound인 연산들은 arithmetic operation보다 메모리 접근을 하는 시간에 의해 실행 시간이 결정되는 연산들을 말한다. 예시로는 element-wise한 연산들이나 reduction(e.g. sum, softmax, batch norm, layer norm) 들이 있다.
일반적으로 연산이 compute-bound인지 memory-bound인지는 해당 연산의 arithmetic intensity, 즉 메모리 접근(바이트) 당 산술 연산의 수를 측정하여 결정한다.
Kernel Fusion
동일한 input에 대해 여러 개의 operation이 순서대로 적용되는 상황이 있다면, 각 operation을 할 때마다 HBM에 load/store를 해야 한다. 이를 한 번만 load 한 후 전체 계산을 fuse해 실행한 후 store하는 것을 kernel fusion이라고 한다.
Kernel fusion은 memory-bound인 operation들의 성능 최적화에 매우 효과적이고, 가장 널리 사용되는 기법이다. 그러나 model training을 할 때는 backward pass를 위해 intermediate value들을 HBM에 쓰는 작업이 필요하기 때문에 naive한 kernel fusion은 효과가 반감된다.
2.2. Standard Attention Implementation
Input $\mathbf{Q}, \mathbf{K}, \mathbf{V}\in\mathbb{R}^{N\times d}$가 주어져 있을 때($N$: sequence length, $d$: head dimension), attention은 다음과 같이 계산된다.
- $\mathbf{S} = \mathbf{Q} \mathbf{K}^T\in \mathbb{R}^{N\times N}$
- $\mathbf{P} = \text{softmax}(\mathbf{S})\in \mathbb{R}^{N\times N}$ (softmax는 row-wise)
- $\mathbf{O} = \mathbf{P}\mathbf{V}\in \mathbb{R}^{N\times d}$
Attention의 표준적인 구현에서는 intermediate matrix들인 $\mathbf{S}$와 $\mathbf{P}$를 HBM에 저장한 후 사용하기 때문에 $O(N^2)$의 공간복잡도를 가지게 된다(일반적으로 $N\gg d$).

논문에서 Algorithm 0이라 부르는 이러한 방식은 대부분의 연산이 memory-bound이기 때문에 실행 시간이 느리고, 특히 attention mask가 곱해지거나 dropout이 추가되는 등의 element-wise 연산이 도입되면 이러한 문제점이 극대화된다. 따라서 이러한 연산들을 fuse하기 위한 방법들이 지속적으로 연구되어 왔다.
3. FlashAttention: Algorithm, Analysis, and Extensions
FlashAttention은 intermediate matrix들을 HBM에 저장하지 않음으로써 HBM 읽기/쓰기 횟수를 줄인 exact attention 구현이다. 이는 메모리를 더 효율적으로 사용하면서도 실행시간 또한 줄이는 효과가 있다.
3.1. An Efficient Attention Algorithm With Tiling and Recomputation
Introduction에서 말했듯, 논문에서는 tiling과 recomputation이라는 두 테크닉을 이용한다. 먼저, $\mathbf{Q}, \mathbf{K}, \mathbf{V}$를 여러 블록으로 쪼개어, HBM에서 이들을 블록 단위로 SRAM에 로드하고 계산하도록 수정한다. 각 블록에서 나온 output에 scaling factor를 곱한 후, 반복문을 돌며 누적해 더하면 최종 결과가 나오게 되는 식이다. 논문에서는 이를 Algorithm 1이라 부른다.
Tiling
먼저 블록 단위로 어텐션을 계산한 후, 각 블록에서 row-wise로 softmax를 계산하여야 한다. Algorithm 1에서는 softmax 계산시 numerical stability를 위해 최대값을 구해 빼준 후 계산을 시행한다. 수식으로 표현하면 $x\in \mathbb{R}^B$에 대해 softmax는 다음과 같이 계산된다.
- $m(x) := \max_i x_i$
- $f(x) := [e^{x_1 -m(x)} \cdots e^{x_B - m(x)}]$
- $l(x) := \sum_i f(x)_i$
- $\text{softmax}(x) = \frac{f(x)}{l(x)}$
이렇게 해서 블록별 softmax를 구해준 후에는 각 블록에 대해 이 $m(x)$와 $l(x)$값을 별도로 저장해둔다. 이를 통해 블록끼리 softmax의 결과를 합쳐 전체의 (row별) softmax 결과를 얻어낼 수 있다.
Recomputation
논문의 목표는 intermediate matrix인 $\mathbf{S}$와 $\mathbf{P}$를 HBM에 저장되지 않도록 하는 것이었다. 그런데 backward pass 시에는 이러한 행렬들이 필요하다.
Algorithm 1에서는 대신 output $\mathbf{O}$와 softmax normalization statistics $(m, l)$, 그리고 SRAM에 올라와 있는 $\mathbf{Q}, \mathbf{K}, \mathbf{V}$의 블록들을 사용해 $\mathbf{S}$와 $\mathbf{P}$를 곧바로 역산해낸다(recomputation). 이는 선택적인 gradient checkpointing의 한 예라고 볼 수 있다.
일반적으로 gradient checkpointing을 도입하면 memory 사용은 줄어들지만, 그만큼 recomputation에 시간이 걸리므로 실행속도가 느려지게 된다. 그러나 여기에서는 그만큼 줄어든 HBM 접근량이 이를 상쇄하고, 오히려 실행속도가 더 빨라지는 효과까지 얻을 수 있다.

위는 Algorithm 1의 pseudocode이다. outer loop의 $j$번째 iteration을 거치고 나면 전체 $\mathbf{Q}$와 $\mathbf{K}_{:j}, \mathbf{V}_{:j}$간의 attention이 $\mathbf{O}$에 저장되는 것으로 이해하면 된다. 코드에 나오는 이중 반복문을 그림으로 나타내면 아래와 같다.
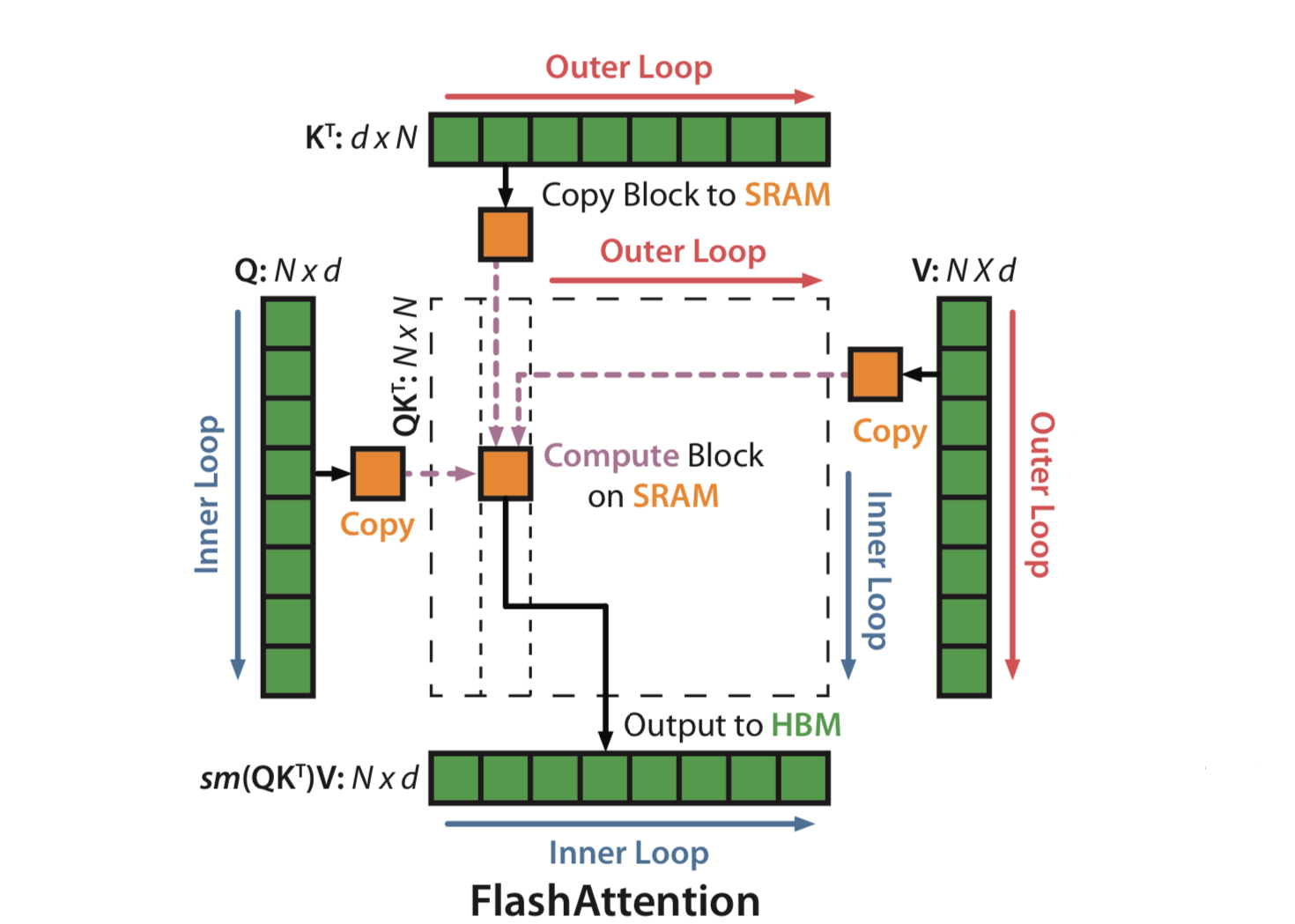
Theorem 1. Algorithm 1 returns $\mathbf{O} = \text{softmax}(\mathbf{Q} \mathbf{K}^T) \mathbf{V}$ with $O(N^2d)$ FLOPs and requires $O(N)$ additional memory beyond inputs and output.
정확성의 증명은 부록에 나와 있다.
3.2. Analysis: IO Complexity of FlashAttention
Algorithm 1에서, $\mathbf{K, V}$의 한 블록은 크기가 $d\times \lceil \frac{M}{4d} \rceil$이므로 점근적으로 $\Theta(M)$의 메모리를 차지한다. 두 행렬의 크기는 각각 $Nd$이므로 블록의 개수는 총 $\Theta(NdM^{-1})$이라 할 수 있는데, 각각의 블록에 대해 반복되면서 $\mathbf{Q}\in\mathbb{R}^{N\times d}$ 전체가 로드되므로 메모리 접근의 수는 총 $\Theta(N^2d^2M^{-1})$가 된다. 이를 조금 더 엄밀하게 증명하여 다음 정리를 얻는다.
Theorem 2. Let $N$ be the sequence length, d be the head dimension, and M be size of SRAM with $d \le M \le Nd$. Standard attention (Algorithm 0) requires $\Theta(Nd+N^2)$ HBM accesses, while FlashAttention (Algorithm 1) requires $\Theta(N^2d^2M^{-1})$ HBM accesses.
일반적으로 $M\gg d^2$이므로 FlashAttention이 Algorithm 0보다 훨씬 메모리 접근을 적게 한다. 또한, 임의의 exact attention algorithm은 점근적으로 FlashAttention보다 메모리 접근을 줄이는 것이 불가능함을 증명할 수 있다.
Proposition 3. Let $N$ be the sequence length, $d$ be the head dimension, and $M$ be size of SRAM with $d\le M\le Nd$. There does not exist an algorithm to compute exact attention with $o(N^2d^2M^{-1})$ HBM accesses for all 𝑀 in the range $[d, Nd]$.
추가로, 논문은 FlashAttention의 실행 시간에서 HBM 접근 수가 determining factor임을 실험적으로 증명한다.
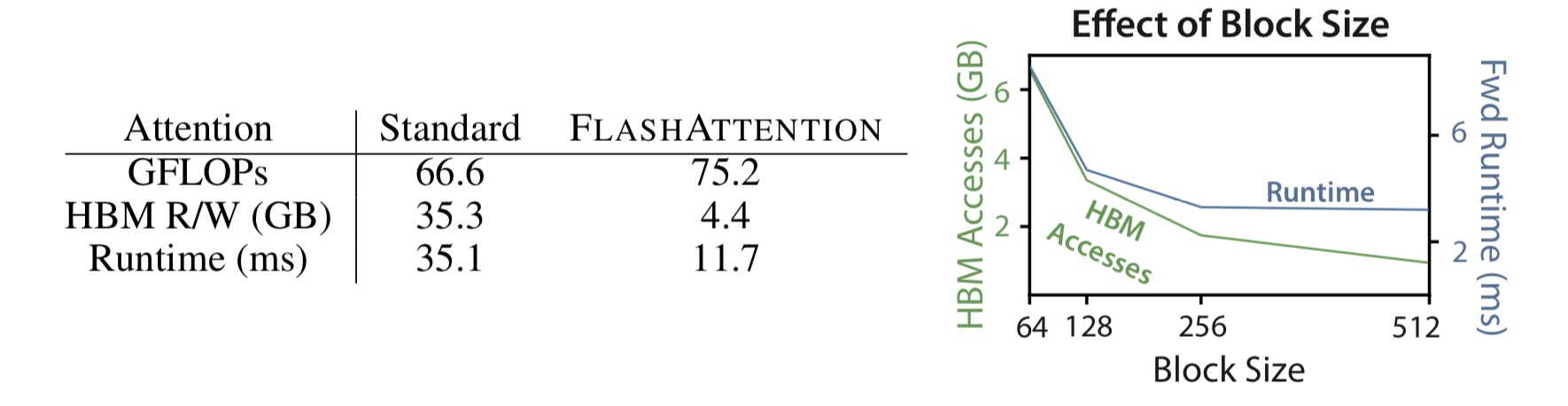
- 왼쪽 그림을 보면, flash attention이 FLOPs 수가 더 많음에도 Standard attention보다 3배 이상 빠른 실행시간을 보여주는 것을 알 수 있다.
- 오른쪽 그림에서는 Block size $B_c$를 조절해가며 HBM access의 수를 줄였을 때 실제로 실행시간이 감소한 것을 확인할 수 있다.
3.3. Extension: Block-Sparse FlashAttention
저자들은 FlashAttention을 확장하여 approximate attention algorithm인 block-sparse FlashAttention을 제어한다. 이는 Algorithm 1과 똑같은 방식으로 작동하지만, mask가 추가로 도입된다는 한 가지만 다르다.
Block-sparse FlashAttention에서는 mask matrix $\mathbf{\tilde{M}}\in{0, 1}^{N\times N}$를 사용해,
$\mathbf{S}=\mathbf{Q} \mathbf{K}^T$, $\mathbf{P} = \text{softmax}(\mathbf{S}\odot \mathbb{1}_{\mathbf{\tilde{M}}})$, $\mathbf{O} = \mathbf{PV}$
가 되도록 계산한다. 이때 mask matrix는 block form으로, $B_r\times B_c$ 크기의 블록들로 나뉘어져 각 블록 내에서는 동일한 값을 가지도록 되어 있다. 이렇게 하면 0인 블록의 attention은 실제로는 계산을 하지 않아도 되고, 그만큼 계산량과 IO complexity를 줄일 수 있게 된다.
Proposition 4. Let $N$ be the sequence length, $d$ be the head dimension, and $M$ be size of SRAM with $d\le M\le Nd$. Block-sparse FlashAttention (Algorithm 5) requires $\Theta(Nd + N^2d^2M^{-1}s)$ HBM accesses where $s$ is the fraction of nonzero blocks in the block-sparsity mask.
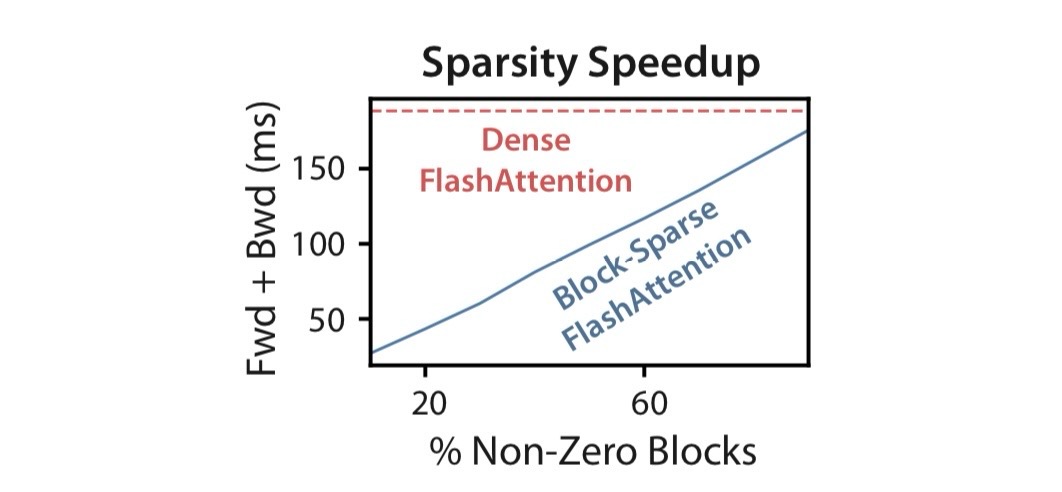
실험 결과를 보면, 위와 같이 mask matrix의 sparsity에 비례하여 실행속도가 빨라지는 것을 알 수 있다. 많은 경우 $s$는 $N^{-1/2}$나 $N^{-1}\log N$으로 설정됨으로써 IO complexity를 $\Theta(N\sqrt{N})$이나 $\Theta(N\log N)$으로 맞추는데 사용된다.
4. Experiments
- Training Speed: FlashAttention으로 여러 모델들을 구현한 결과, 기존 기록보다 BERT를 15%, GPT-2를 HuggingFace보다 3배 빠르게 실행시키는 등의 결과를 얻었다.
- Quality: 메모리를 덜 차지함으로써 FlashAttention은 더 긴 context length를 가질 수 있고, 이를 통해 long-document classification 등의 작업에서 최고기록을 경신하였으며 Path-X에서 최초로 better-than-random performance를 달성하였다.
-
Benchmarking Attention:
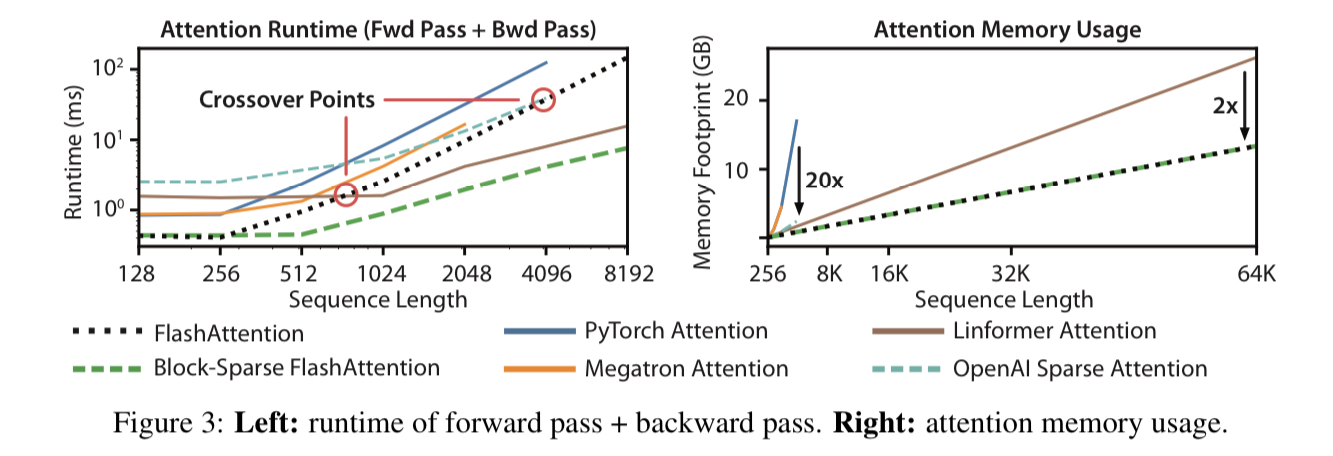
- FlashAttention의 경우 실행 시간은 $O(N^2)$로 기존 구현과 동일하지만, PyTorch 구현보다 최대 3배 빠르게 실행되는 등 유의미한 실행속도 향상을 확인할 수 있다.
-
Block-sparse FlashAttention은 exact와 approximate을 가리지 않고 알려진 모든 attention 방법들 중 가장 빠른 성능을 보여주었다.
-
메모리 사용량을 비교해보면 기존보다 최대 20배 적은 메모리를 사용하며 심지어는 approximate attention algorithm들과 비교해도 최대 2배 메모리를 적게 사용하였다. block-sparse FlashAttention도 그냥 FlashAttention과 메모리 사용량은 같음을 확인할 수 있다.
5. Limitations and Future Directions
FlashAttention은 IO-aware한 구현을 위해 CUDA kernel을 직접 구현해야 한다는 불편함이 있다. 이는 PyTorch 등 프레임워크를 사용하는 것보다 훨씬 많은 노력을 요구한다는 한계가 있다.
저자들은 이 논문이 transformer 외에도 다른 딥러닝 모듈들을 IO-aware하게 만드는 데 영감을 주기를 기대하며, 현재는 단일 GPU 환경에서만 사용가능한 FlashAttention을 multi-GPU 환경으로 확장하는 것을 향후 연구과제로 남겨둔다.