[논문 정리] A White Paper on Neural Network Quantization

March 14, 2024, 12:24 p.m. · 16 min read · 🌐︎ ko

deep learning network quantization paper review

Nagel, M., Fournarakis, M., Amjad, R. A., Bondarenko, Y., Van Baalen, M., & Blankevoort, T. (2021). A white paper on neural network quantization. arXiv preprint arXiv:2106.08295.

Qualcomn에서 출판한 quantization 관련 리뷰 논문이다.

Abstract

최근 뉴럴 네트워크들이 다양한 장치들에 적용되고 있으며, 이를 위해서는 NN의 높은 computational cost를 줄이는 작업이 필요하다. 특히 inference time의 power와 latency를 줄여야 이러한 edge device에 NN을 적용하는 것이 가능하다. Neural Network Quantization은 이를 위해 매우 효과적인 방법이다.

이 논문에서는 weight와 activation fn을 low-bit로 유지하면서도 quantization noise의 impact를 최소화하는 SOTA 알고리즘들을 소개한다. 일반적으로 quantization의 방법론들은 두 가지로 나뉠 수 있는데, Post-Traning Quantization과 Quantization-Aware Training이다.

  1. PTQ는 re-training이나 labelled data가 필요하지 않아 간단하다. 8-bit quantization 정도는 거의 성능 하락 없이 해낼 수 있다.
  2. 반면 QAT는 fine-tuning이 필요하고 labelled data를 요구하지만 더 적은 비트로 quantize가 가능하다.

본 논문에서는 각각의 솔루션에 대해 표준적인 training pipeline을 제시하고 실험을 진행한다.

1. Introduction

최근 몇 년간 뉴럴 네트워크를 스마트폰이나 가전제품 등 다양한 전자제품에 탑재하려는 시도가 끊이지 않아왔다. 그런데 일반적으로 이러한 장치들은 보통 inference 실행 시간과 에너지에 제약이 있다. Neural Network Quantization은 이를 해결하기 위한 좋은 방법으로, layer weight와 activation(각 layer의 output) tensor를 (일반적인) 16, 32-bit floating point보다 낮은 precision으로 저장하여 computational cost를 낮춘다.

일반적으로 뉴럴네트워크는 quantization에 robust한 것으로 알려져있다. 즉, quantization을 해도 성능에 영향이 적다. 그러나, 더 적은 수의 비트로 quantization시 noise로 인해 성능이 하락할 수도 있으며 후술할 특정 네트워크들에서는 성능에 영향 최소화하기 위해 각별한 노력이 필요하다.

SOTA network quantization을 살펴보는 이 논문에서는 먼저 quantization에 대한 소개와 함께 이를 위한 하드웨어와 practical consideration들을 살펴본다. 이후 quantization을 위한 두 가지 방법론인 Post-Training Quantization(PTQ)과 Quantization-Aware Training(QAT)을 소개한다.

논문은 두 방법론에 대해 표준적인 절차를 정리해 제공하고, 디버깅 절차와 흔히 발생하는 이슈들을 정리해 알려준다.

2. Quantization Fundamentals

이 장에서는 NN Quantization에 대한 기본적인 원리를 소개한다. 우선 하드웨어적 motivation을 설명하고, 표준적인 quantization scheme과 그 성질들을 짚고 넘어간다. 또, 뉴럴 네트워크에 흔히 등장하는 layer들이 실제 quantization을 거쳤을 때의 practical consideration들을 짚어준다.

2.1. Hardware Background

우리가 Quantization을 하는 이유는 neural network accelerator가 행렬/벡터 연산 $\mathbf{y} =\mathbf{Wx}+\mathbf{b}$를 처리하는 방식과 연결되어 있다. 이러한 행렬 연산들은 뉴럴 네트워크 계산에서 가장 기본적인 요소로, NN accelerator는 이러한 연산을 최대한 병렬화시켜 처리하는 것을 목표로 한다.

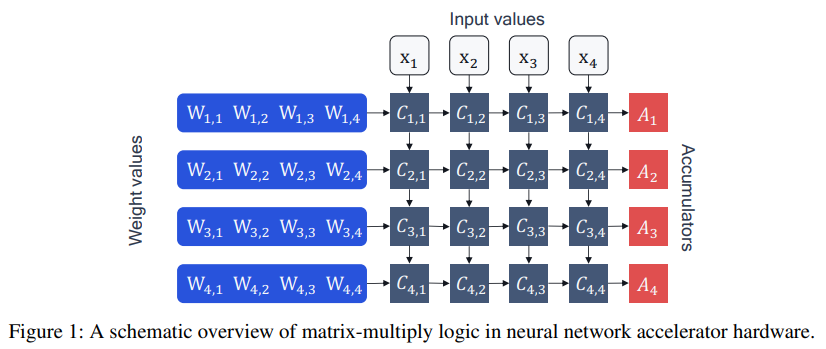
Figure 1.과 같이 NN accelerator는 processing element $C_{n,m}$과 accumulator $A_n$으로 구성되어 있다. 그림은 16개의 processing element가 4x4의 grid로 배열되어 4개의 accumulator에 누적되도록 배치되어 있는 것으로, 이는 연산을 다음과 같은 방법으로 수행한다.

  1. accumulator에 bias값 $\mathbf{b_n}$을 불러온다.
  2. Weight 값 $\mathbf{W_{n, m}}$과 input value $\mathbf{x}_m$을 불러온다.
  3. array의 각 processing element에서 곱셈 $C_{n, m} = \mathbf{W}_{n, m}\mathbf{x}_m$을 수행한다.
  4. 계산 결과들이 accumulator에서 $A_n = \mathbf{b}_n + \sum_m C_{n, m}$ 와 같이 합산된다. 이를 Multiply-ACcumulate(MAC)이라고 한다.
  5. 계산 과정이 끝나면 결과가 메모리로 다시 옮겨지고, NN의 다음 layer에서 사용된다.

이러한 계산 과정 중에서는 MAC 연산, 그리고 데이터를 processing unit과 메모리 사이에서 옮기는 부분이 많은 에너지를 소모한다. 따라서 lower bit로 quantization을 수행하면 많은 에너지를 절감할 수 있다. 특히 INT8과 같이 fixed-point로 quantize를 진행한다면 메모리를 아낄 수 있을뿐만 아니라 곱셈 연산이 floating point에 비해 더 효율적이므로 에너지 소비를 더 낮출 수 있다.

따라서 우리는 부동소수점들로 이루어진 벡터를 정수 벡터로 바꾸기 위한 scheme이 필요하다. Floating point vector $\mathbf{x}$는 근사적으로 다음과 같이 표현할 수 있다.

$$\hat{\mathbf{x}} = s_ \mathbf{x} \cdot \mathbf{x}_{\text{int}} \approx \mathbf{x}$$

여기서,

따라서 MAC 연산은 다음과 같이 표현할 수 있다.

$$\hat{A_n} = \hat{\mathbf{b}}_n + \sum_m \hat{\mathbf{W}} ^{\text{int}}_{n, m} \hat{\mathbf{x}}_m$$

$$=\hat{\mathbf{b}}_n + \sum_m (s_\mathbf{W}\hat{\mathbf{W}}^{\text{int}}_{n, m}) (s_\mathbf{x}\hat{\mathbf{x}}_m)$$

$$=\hat{\mathbf{b}}_n + s_\mathbf{W} s_\mathbf{x}\sum_m \hat{\mathbf{W}}^{\text{int}}_{n, m}\hat{\mathbf{x}}_m$$

Bias는 일반적으로 quantize되지 않기 때문에 그대로 두었다. 또한, input들과 weight를 quantize했다고 해도 accumulator 자체는 32비트에서 동작해야 한다는 것을 명심해야 한다. accumulator의 출력은 덧셈이 모두 끝난 후 requantization 과정을 거쳐 저장된다.

2.2. Uniform affine quantization

본 논문에서 다룰, 그리고 가장 널리 쓰이는 quantization scheme은 uniform quantization이다. fixed-point arithmetic으로 자연히 이어지기 때문이다.

먼저 uniform affine quantization(또는 asymmetric quantization)은 다음의 세 파라미터로 결정된다.

이 세 파라미터가 결정되면 실수 벡터 $\mathbf{x}$는 unsigned integer grid에서

$$\mathbf{x}_{\text{int}} = \text{clamp}\left(\lfloor \frac{\mathbf{x}}{s}\rceil + z;0;2^b-1\right)$$

매핑할 수 있다. 여기서 $\lfloor \rceil$은 round-to-nearest 연산을 의미한다. 반대로 dequantization은 $\mathbf{x}\approx \mathbf{\hat{x}}=s(\mathbf{x}_\text{int}-z)$로써 가능하다.

다음은 uniform affine quantization의 특수한 경우들이다.

Quantization Granularity
Quantization을 할 때는 일반적으로 weight tensor의 파라미터마다, activation vector마다 동일한 quantizer를 사용한다(per-tensor quantization). 반면 동일 tensor 내에서도 채널별로 다른 quantizer를 사용하는 것도 가능한데, 이렇한 경우를 per-channel quantization이라고 하고 quantization의 granularity를 증가시켰다고 말한다.

Granularity가 증가하면 일반적으로 정확도가 올라가지만, accumulator가 채널마다 scale을 달리 해가며 계산해야 하므로 계산시 비용이 높아진다.

2.3. Quantization Simulation

Quantize된 네트워크가 잘 작동할지를 판별하기 위해, 많은 경우 네트워크 훈련과 동일한 환경에서 quantization을 시뮬레이션하게 된다. 이 경우 실제 디바이스에서 quantize된 값들로 계산이 이루어지는 과정을 floating point로 모사하여 계산을 진행하면 된다. 이 섹션에서는 시뮬레이션 시의 성능과 실제 on-device 성능의 차이를 최소화할 수 있는 방법들을 다룬다.

Batch Normalization Folding
Batch normalization은 선형 연산이기 때문에, 마찬가지로 선형인 행렬 곱 연산에 흡수시킬 수 있다. 이렇게 하면 inference시에는 BN이라는 계층 자체가 없어지는 것이 되며, 계산의 overhead를 줄이고 불필요한 데이터의 이동을 줄이는 효과가 있다. 또한, BN을 한 후 다시 quantization을 함으로써 생기는 성능 감소를 줄일 수 있다.

Activation Function Fusing
Linear layer 후에 nonlinear activation function이 나오는 경우, linear layer의 출력을 quantize하지 않고 바로 activation을 적용하는 것이 낫다. 이렇게 linear layer와 뒤따르는 activation function을 합쳐버리는 것을 activation function fusing이라고 한다. 일반적으로 quantization시 ReLU가 아닌 sigmoid나 Swish 등의 활성화 함수는 거의 사용되지 않는데, 구현 과정이 복잡해지고 fixed-point에서는 그렇게 효과적이지도 않기 때문이다.

Other Layers and Quantization

2.4. Practical Considerations

Quantization을 할 때에는 quantization scheme, granularity, bit width 등 방대한 parameter space에서 선택을 해야 한다. 이 섹션에서는 search space를 줄이기 위한 조언들을 다룬다.

Symmetric vs. Asymmetric Quantization
일반적으로 activation은 asymmetric하게, weight는 symmetric하게 quantize한다. 만약 둘 모두가 asymmetric하다면 $\hat{\mathbf{W}} \hat{\mathbf{x}}$를 계산하는 과정에서 zero point를 보정해주느라 추가적인 계산을 하게 되어 overhead가 발생한다. Activation만 asymmetric하게 한다면 최소한의 overhead로 표현력 향상에 따른 성능 향상이 가능하다.

Per-tensor and Per-channel Quantization
일반적으로는 per-tensor quantization이 오랜 표준으로 사용된다. 그러나 하드웨어가 이를 지원할 경우, weight를 per-channel quantize한다면 성능이 향상되는 경우가 많다. 이는 NN accelerator가 채널마다 다른 scale factor를 사용함으로써 가능하다. 반면 per-channel activation의 구현은 훨씬 어렵고, MAC에서 $s_\mathbf{x}$로 곱셈의 전체 계산값을 묶을 수 없게 됨으로써 발생하는 비효율이 훨씬 크다.

3. Post-Training Quantization

PTQ는 FP32에서 훈련한 네트워크를 그대로 가져와 fixed-point화 시키는 과정이다. 이 장에서는 quantization parameter를 잘 찾기 위한 방법들을 찾아보고, PTQ를 위한 표준적인 파이프라인을 제공한다. 또한 모델이 잘 작동하지 않을 경우 사용할 수 있는 디버깅 방법도 서술한다.

3.1. Quantization Range Setting

Quantization range를 찾을 때는 clipping과 rounding error 사이의 trade-off가 존재한다. 일반적으로는 min-max, MSE, cross entropy 등의 방법을 사용해 quantization error를 찾게 된다.

$$\argmin_{q_\text{min}, q_\text{max}} H(\psi(\mathbf{v}), \psi(\mathbf{\hat{v}}(q_\text{min}, q_\text{max})))$$

를 이용해 quantization range를 설정한다. 여기서 $H$가 cross-entropy, $\psi$는 softmax 함수이다.

$$q_\text{min}=\min(\beta-\alpha \gamma), \quad q_\text{max} \min(\beta+\alpha \gamma)$$

로 설정하여 range를 정하면 min-max보다 outlier에 덜 취약하면서도 간단하게 range를 설정할 수 있다.

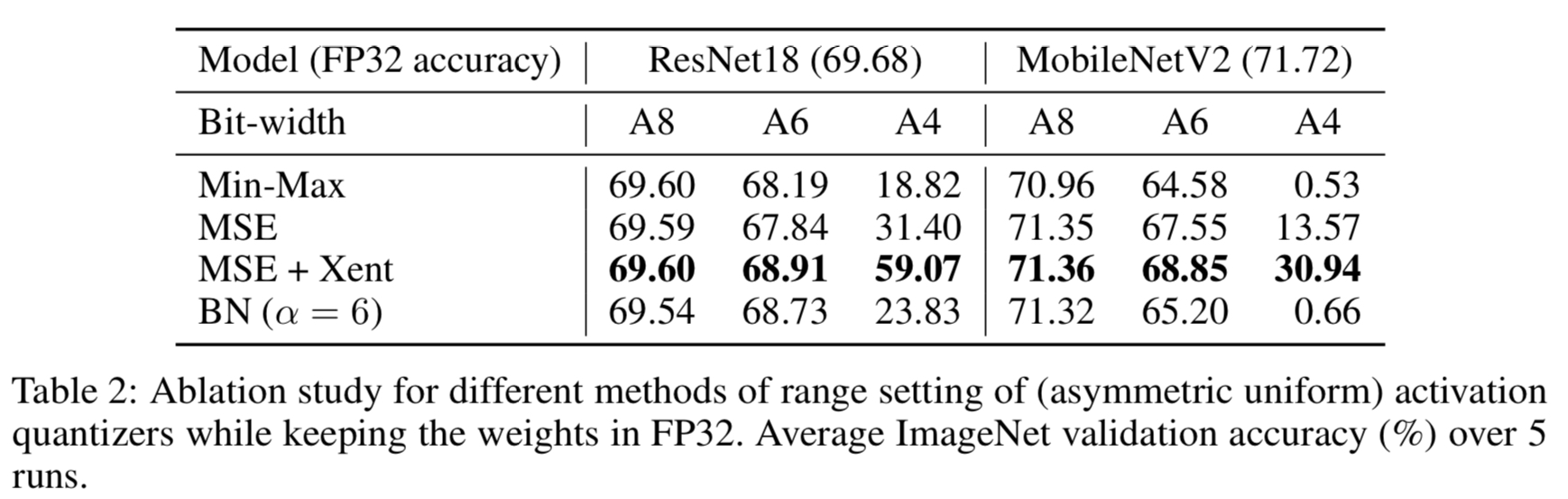
Table 2.를 보면, lower bit로 갈수록 min-max는 성능이 급격하게 떨어지며, MSE가 훨씬 나은 결과를 보여준다. 또한, 마지막 계층에만 Cross Entropy를 사용한 경우(MSE+Xent)가 특히 lower bit에서는 다른 방법에 비해 훨씬 좋은 성능을 보임을 알 수 있다.

3.2. Cross-Layer Equalization

Quantization 과정에서 발생가능한 흔한 문제점 중 하나는 동일 tensor 내에서 원소간의 magnitude 차이가 너무 클 수 있다는 것이다. 이 경우 clipping과 rounding error 사이 trade-off에서 좋은 선택지가 없을 가능성이 커진다. 특히 MobileNetV1과 같이 depth-wise separable convolution 등의 계층이 있는 경우, per-tensor granularity 채택 시 tensor 내 magnitude 차이로 인한 성능 하락이 크게 발생한다.

Per-channel quantization 없이 이를 해결하기 위한 방법으로 cross-layer equalization(CLE)이 있다. CLE는 먼저 ReLU나 PreLu와 같은 많은 activation function이 positive scaling equivariance라는 성질을 만족한다는 관측에서 시작된다.

$$f(sx) = sf(x)\quad (s>0)$$

두 linear layer $\mathbf{h}=f(\mathbf{W^{(1)}}\mathbf{x} + \mathbf{b}^{(1)})$, $\mathbf{y}=f(\mathbf{W^{(2)}}\mathbf{h} + \mathbf{b}^{(2)})$가 있고 그 사이에 이러한 성질을 만족하는 activation function이 있다고 하자. 이때 다음이 성립하게 된다.

$$\mathbf{y}=f(\mathbf{W^{(2)}}f(\mathbf{W^{(1)}}\mathbf{x} + \mathbf{b}^{(1)}) + \mathbf{b}^{(2)})$$

$$=f(\mathbf{W^{(2)}}\mathbf{S}f(\mathbf{S}^{-1}\mathbf{W^{(1)}}\mathbf{x} + \mathbf{S}^{-1}\mathbf{b}^{(1)}) + \mathbf{b}^{(2)})$$

$$=f(\mathbf{\tilde{W}^{(2)}}f(\mathbf{\tilde{W}^{(1)}}\mathbf{x} + \mathbf{\tilde{b}}^{(1)}) + \mathbf{b}^{(2)})$$

여기에서 $\mathbf{S} = \text{diag}(\mathbf{s})$는 대각행렬이다. 즉, 아래쪽 layer $\mathbf{W^{(1)}}$를 row별(i. e. output channel별)로 scale down하고 그만큼 위쪽 layer $\mathbf{W^{(2)}}$를 scale up한다고 볼 수 있다. 연구에 따르면

$$\mathbf{s}_i = \frac{1}{\mathbf{r}_i^{(2)}} \sqrt{\mathbf{r}_i^{(1)}\mathbf{r}_i^{(2)}}$$

인 경우 최적의 weight equalization이 이루어진다고 한다.

Absorbing High Biases
특히 CLE를 한 후의 경우, 높은 bias는 activation의 dynamic range에서 큰 편차를 낳을 수 있다. 이를 방지하기 위해서 CLE와 유사하게 bias를 다음 layer에 흡수시킬 수 있다.

$$\mathbf{y}=f(\mathbf{W^{(2)}}\mathbf{h} + \mathbf{b}^{(2)})$$

$$=f(\mathbf{W^{(2)}}(f(\mathbf{W^{(1)}}\mathbf{x} + \mathbf{b}^{(1)}) + \mathbf{c} -\mathbf{c}) +\mathbf{b}^{(2)})$$

$$=f(\mathbf{W^{(2)}}(f(\mathbf{W^{(1)}}\mathbf{x} + \mathbf{\tilde{b}}^{(1)}) + \mathbf{c}) +\mathbf{b}^{(2)})$$

$$=f(\mathbf{W^{(2)}}f(\mathbf{W^{(1)}}\mathbf{x} + \mathbf{\tilde{b}}^{(1)}) +\mathbf{\tilde{b}}^{(2)})$$

이 때 두 번째에서 세 번째 수식으로 넘어갈 때에는, ReLU가 제한된 범위의 $x$에 대해서는 $f(x-c) = f(x) - c$를 성립시킨다는 점에서 착안한다. 즉 $x$의 분포가 주어져 있을 때 이것이 성립하도록 $c$를 잘 찾아야 하는데, 이는 아래와 같다.

$$\mathbf{c}_i = \max\left(0, \min_x \left(\mathbf{W}_i^{(1)}\mathbf{x} + \mathbf{b}_i^{(1)}\right)\right)$$

여기에서 $\min_x$는 주어진 분포의 $x$에 대해 evaluate되는 것으로, 엄밀한 최소값이라기보다는 empirical minimum을 의미한다. 만약 layer 1이 BN을 거친다면, minimum을 간단히 $\mathbf{\beta}_i - 3\mathbf{\gamma}_i$로 잡아 $\mathbf{c}_i = \max(0, \mathbf{\beta}_i - 3\mathbf{\gamma}_i)$라 할 수도 있다.

Experiments

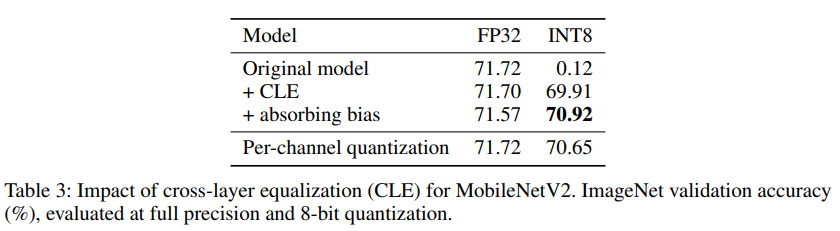
실험 결과, depthwise separable convolution이 적용된 MobileNetV2의 경우 INT8로 per-tensor quantize되었을 때 CLE가 적용되지 않으면 0에 가까운 정확도를 보인 것을 알 수 있다. 반면 CLE를 적용하면 성능이 대폭 상승하는 것을 확인할 수 있다.

3.3. Bias Correction

Quantization 시 발생할 수 있는 흔한 이슈 중 하나는 quantization error가 편향되는 현상이다. 즉, 네트워크의 한 layer에서 quantization을 적용하기 전과 후에 기대값이 달라지는 것이다.

$$\mathbb{E}[\mathbf{Wx}]\ne \mathbb{E}[\mathbf{\hat{W}\hat{x}}]$$

가 되는 현상이다. 이는 일반적으로 한쪽 방향의 outlier만 quantization 과정에서 절삭되면서 발생한다. 이러한 오차를 계산하여 교정하기 위한 방법을 bias correction이라고 한다. 우선 이를 위한 수학적 배경을 먼저 살펴보자. Linear layer의 weight 행렬을 $\mathbf{\hat{W}}$이라고 할 때, quantization에 의해 발생한 오차를 $\Delta \mathbf{W} = \mathbf{\hat{W}} - \mathbf{W}$이라고 두자. 그러면

$$\mathbb{E}[\mathbf{y}]=\mathbb{E}[\mathbf{\hat{W}x}] = \mathbb{E}[(\mathbf{\hat{W}} + \Delta \mathbf{W})\mathbf{x}]$$

$$= \mathbb{E}[\mathbf{\hat{W}}\mathbf{x}] + \mathbb{E}[\Delta \mathbf{W}\mathbf{x}] $$

이므로 biased error는 $\mathbb{E}[\Delta\mathbf{W}\mathbf{x}] = \Delta\mathbf{W} \mathbb{E}[\mathbf{x}]$로 나타낼 수 있다. 즉 이만큼을 layer output에서 빼주어야 quantize하지 않았을 때와 기댓값이 같아진다. 이 $\Delta\mathbf{W} \mathbb{E}[\mathbf{x}]$를 어떻게 추정하냐에 따라서 Bias correction의 방법이 두 가지로 크게 나뉘어 진다.

Empirical Bias Correction

Calibration Dataset에 접근할 수 있는 경우, 단순히 full precision model과 quantized model에서의 activation의 평균값을 실험적으로 각각 구해 빼주어 이를 계산할 수 있다.

Analytic Bias Correction
추가적인 데이터 없이도 bias correction을 진행할 수 있는 방법이다. 이는 해당 linear layer에 들어오는 입력값이 정규분포를 따르는 벡터에 Batch Normalization과 ReLU가 적용된 것이라고 가정한다.

그러면 linear layer의 입력 $\mathbf{x}$는 BN의 결과로 평균이 $\gamma$, 표준편차가 $\beta$가 된 상태($\mathbf{x}^\text{pre}$)에서 ReLU를 씌운 것($\text{ReLU}(\mathbf{x}^\text{pre})$)이 된다. $\mathbf{x}$의 분포로 기대값을 구하면

$$\mathbb{E}[\mathbf{x}] = \mathbb{E}[\text{ReLU}(\mathbf{x}^\text{pre})] $$

$$=\gamma \mathcal{N}\left(\frac{-\beta}{\gamma} \right) +\beta \left[1-\Phi\left(\frac{-\beta}{\gamma}\right)\right]$$

가 됨이 알려져있고, $\Delta \mathbf{W}$에 이를 곱함으로써 quantization bias를 구할 수 있다. 이를 빼주어 보정해주면 된다.

Experiments

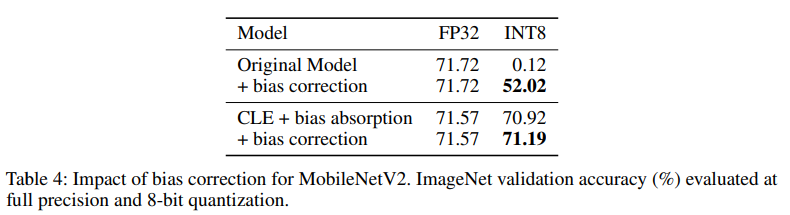
Table 4는 MobileNetV2에 bias correction이 적용되기 전과 후의 성능 변화를 비교해 보여준다. INT8로 quantize시, bias correction 없이는 random에 가깝던 output이 52.02%의 정확도까지 올라간 것을 알 수 있다.

또한 Cross Layer Equalization과 bias absorption이 이미 적용되어 있는 상태에서도 bias correction을 추가로 적용할 시 성능이 소폭 상승하는 것 또한 확인할 수 있다.

3.4. AdaRound

주어진 quantizer로 네트워크를 quantize할 때에는 일반적으로 텐서의 각 값을 quantization grid상에서 가장 가까운 값으로 매핑시킨다. 이를 rounding-to-nearest라고 한다. 그런데 이러한 전략은 텐서의 quantization 전후간 MSE를 최소화하는 것일 뿐, task의 전체 성능까지 최적화하는 것은 아니다. AdaRound는 rounding-to-nearest 대신에 사용할 수 있는 빠르고 간단한 rounding scheme이다.

quantization의 목표는 원래의 floating-point 네트워크와 비교해 일어나는 성능 감소를 최소화하는 것이다. 즉,

$$\argmin_{\Delta \mathbf{w}} \mathbb{E}\left[ \mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{w}+\Delta \mathbf{w}) - \mathcal{L}(\mathbf{x}, \mathbf{y}, \mathbf{w})\right]$$

에 해당하는 $\Delta \mathbf{w}$를 찾는 것이 rounding scheme들의 목표라고 할 수 있다. 여기서 $\Delta \mathbf{w}$는 각 element에 비해 rounding up과 down의 두 가지가 있으므로 $2^n$($n$은 $\mathbf{w}$의 차원)가지 중 하나가 된다.

AdaRound는 위의 식을 Taylor 2차 근사한 후, 두 가지 가정을 적용하여 식을 단순화시킬 수 있다.

  1. 훈련 과정에서 loss function이 완전히 수렴하였다고 가정한다. 즉, $\nabla_{\mathbf{w}} \mathcal{L}=0$을 가정한다.

  2. 서로 다른 layer에 속한 weight들 사이의 상호작용은 존재하지 않는다. 즉, $H_\mathbf{w}\mathcal{L}$은 block diagonal이다.

    • $\mathbf{w}$는 네트워크의 모든 layer의 매개변수들을 일렬로 나열한 벡터라고 가정하면 이해가 된다. layer $i$의 파라미터로 미분한 후 layer $j(\ne i)$의 파라미터로 미분하면 0이 되어야 하기 때문이다.

그러면 위의 최적화 문제는 아래의 quadratic unconstrained binary optimization(QUBO) 문제로 변형된다.

$$\argmin_{\Delta \mathbf{w}^{(l)}} \mathbb{E}\left[ \Delta {\mathbf{w}^{(l)}}^T \mathbf{H}^{(\mathbf{w}^{(l)})} \Delta {\mathbf{w}^{(l)}} \right]\; l=1, \cdots, L$$

논문은 실제로 이러한 quadratic term의 값을 줄이는 것이 성능과 유의미한 상관관계가 있음을 보여준다. 그런데 이 문제 또한 해결하는 방법이 NP-hard임이 알려져 있으며, loss function의 hessian을 계산하는 것 또한 메모리와 계산의 효율성 측면에서 비효율적이다.

따라서 추가적인 가정들을 도입하면(논문에서는 생략), 위의 문제를 다음의 local optimization problem으로의 간단화가 가능하다. 이는 각 layer의 output에서 quantization error의 MSE를 최소화하는 것과 같다.

$$\argmin_{\Delta \mathbf{W}_k^{(l)}} \mathbb{E}\left[(\Delta \mathbf{W}_{k,:}^{(l)}\mathbf{x}^{(l-1)})^2\right]$$

위 최적화 문제의 경우 hessian을 구할 필요도, back/forward propagation을 할 필요도 없다. 그러나 $2^n$가지의 경우의 수를 모두 따져봐야 한다는 점에서 여전히 NP-hard 문제이다. 따라서 근사해를 구하는 데서 만족하기로 하고, 최적화 문제를 완화(relax)하고 activation function을 적용해 다음과 같이 바꿔놓을 수 있다.

$$\argmin_{\mathbf{V}} \lVert f_a(\mathbf{Wx})-f_a(\mathbf{\tilde{W}}\mathbf{x}) \rVert_F^2 + \lambda f_{reg}(\mathbf{V})$$

이때 $\tilde{\mathbf{W}} = s\cdot \text{clamp}\left(\lfloor\frac{\mathbf{W}}{s}\rfloor + h(\mathbf{V});n,p\right)$이고, $h$는 0과 1 사이의 값을 가지는 monotonic function으로 sigmoid등이 사용된다. $f_{reg}$는 $h$가 0과 1 중 하나의 값에 근접하도록 유도하는 regularization term으로,

$$f_{reg}(\mathbf{V}) = \sum_{i, j} 1 - |2h(\mathbf{V}_{i, j})-1|^\beta$$

로 정의되며 $\beta$가 optimization process가 진행됨에 따라 점점 증가하며 더 강하게 enforce하는 작용을 한다. 이러한 방법으로 weight rounding을 최적화하는 방법을 AdaRound라고 한다.

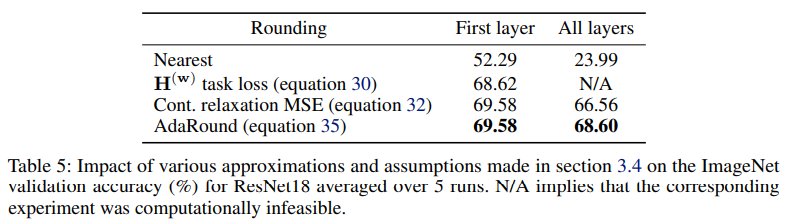
위 Table 5를 보면, 4-bit로 quantize하였을 때 rounding-to-nearest보다 AdaRound를 사용하였을 때 성능에 획기적인 향상이 있는 것을 알 수 있다. 특히, hessian을 이용한 최적화 방정식이나 각 output의 quantization error의 MSE를 최소화하는 것보다도 오히려 그 근사 방법인
AdaRound가 더 좋은 성능을 보임을 확인할 수 있다.

3.5. Standard PTQ Pipeline

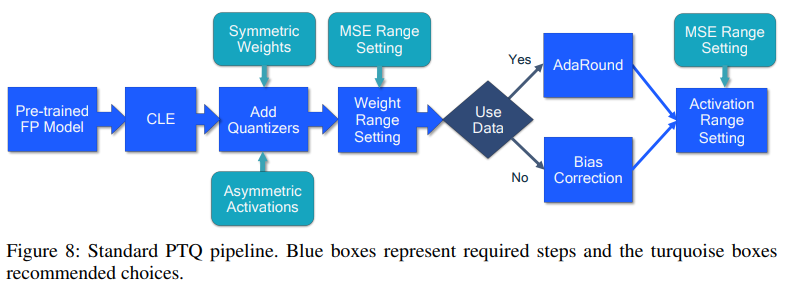
앞에서 살펴본 실험들에 근거해, 논문에서는 Post-Training Quantization을 위한 표준적인 pipeline으로 위의 그림과 같은 방법을 제시한다.

3.6. Experiments

위의 pipeline을 사용하여 비전과 NLP의 여러 모델을 quantize시키고 성능을 비교하는 섹션이다.

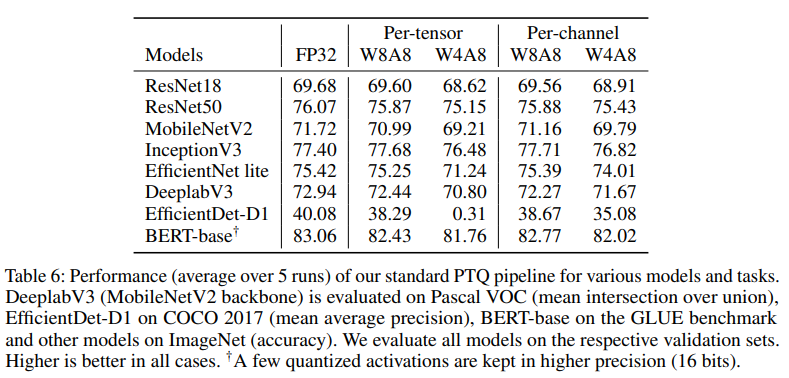
결과를 보면, weight와 activation을 모두 8bit로 quantize한 경우(W8A8)에는 성능의 저하가 거의 일어나지 않는 것을 확인할 수 있다. 또한, per-channel quantization이 주는 성능 향상은 W8A8까지는 미미함을 알 수 있다. 다만 W4A8까지 압축시킨 경우, EfficientNet lite 등 depth-wise separable convolution을 사용한 모델들에서는 per-channel quantization이 유의미한 성능 변화를 주었다. 특히 EfficientDet-D1의 경우 W4A8에서 per-tensor로 quantize하였을 때는 유의미한 예측 자체를 내놓지 못했다.

3.7. Debugging

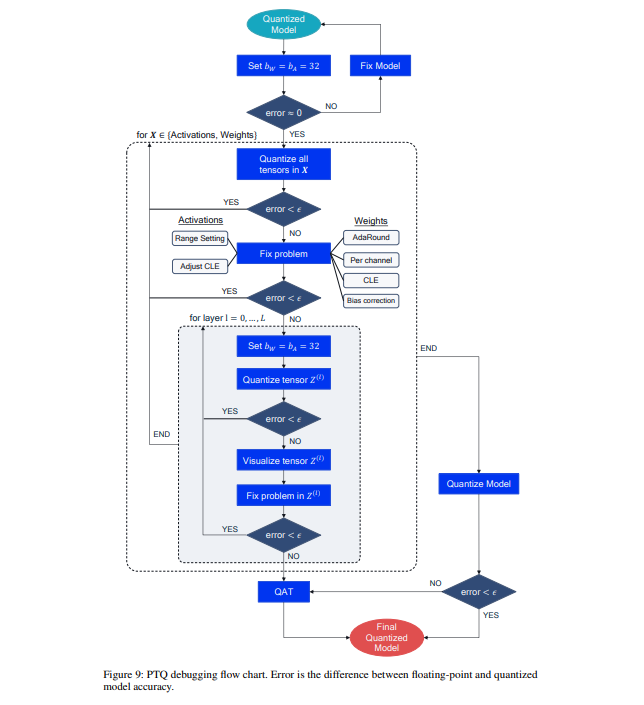
논문에서는 모델을 quantize했음에도 불구하고 성능이 잘 나오지 않는 경우, 이를 해결하기 위해서 어떻게 해야 하는지 debugging step 또한 제시한다. 이는 위의 Figure 9에 요약되어 나타나 있다.

4. Quantization-Aware Training

Quantization-Aware Training(QAT)의 경우 PTQ와는 대비되는 개념으로 training단계에서부터 quantization을 고려한다. 즉 PTQ와는 달리 데이터에 접근이 가능하고, 투입가능한 계산자원과 시간이 여유로울 때 사용할 수 있다. PTQ만 사용해도 W8A8정도로 quantization을 하는 것은 문제가 없으나, 그보다 낮은 비트로 quantize를 하면서도 성능 저하를 최소화하기 위해서는 QAT가 유리하다.

4.1. Simulating Quantization for Backward Pass

Quantization이 적용된 상태에서 네트워크를 훈련시키는 경우 가장 먼저 미분이 불가능해진다는 문제점에 봉착한다. 일반적으로 QAT에서는 이를 straight-through estimator(STE)라는 방법을 통해 해결한다. 이는 rounding operator의 미분을

$$\frac{\partial \lfloor y\rceil}{\partial y} = 1$$

로 근사하는 것이다. STE 근사를 사용하면

$$\frac{\partial \mathbf{\hat{x}}_i}{\partial \mathbf{x}_i}=\begin{cases}1&\text{if } q_{min} \le \mathbf{x}_i\le q_{max} \\ 0 & \text{otherwise}\end{cases}$$

가 된다. 즉, backward propagation을 할 때에는 quantizer를 건너뛰어도 된다는 결론을 얻는다.

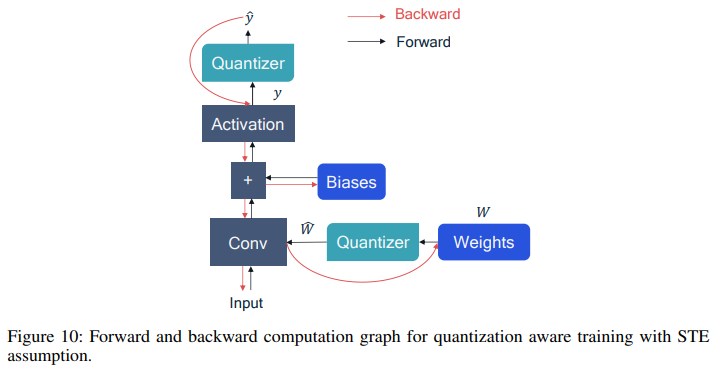
Figure 10의 계산 그래프는 forward pass와 backward pass시 계산이 어떻게 이루어지는지를 표현한 것이다.

한편, STE 가정은 quantization parameter인 $s$와 $z$에 대한 gradient를 구하는 데도 사용될 수 있다. 이를 사용하며 quantization parameter들 또한 learnable하게 바꾸는 것이 가능하다.

4.2. Batch Normalization Folding and QAT

Lower-bit를 시뮬레이션하여 훈련을 진행할 때에는 batch normalization folding에 대한 고려가 필요하다. BN folding은 기본적으로 training때가 아닌 inference 시에 적용되는 기법이기 때문이다. Training시에는 BN folding을 하지 않다가 inference시에만 적용한다면 새로운 quantization noise의 영향으로 성능이 하락할 수 있기 때문이다. 이는 특히 per-tensor quantization이 적용되었을 때 문제가 된다.

QAT에서 BN folding 문제를 해결하기 위해서는 일반적으로 BN scale을 statically fold하는 방법이 널리 사용된다. 사전학습된 모델의 Batch Normalization parameter를 상수로 취급해 BN folding을 한 상태로 QAT를 시작하는 것이다. 이외에도 QAT와 BN-folding을 번갈아가면서 진행하는 방법이 있으나, 단순 static-folding과 성능 차이가 없으며 forward pass를 두 번 해야 하기 때문에 잘 쓰이지 않는다.

Per-channel Quantization
반면 per-channel quantization이 적용된 경우에는 training 시에는 batch normalization layer를 그대로 두고, inference 시에만 이를 quantizer의 scaling factor에 합치면 된다. Batch Normalization 또한 channel-wise로 작용하는 선형변환이기 때문에, 마찬가지로 channel-wise linear transform인 quantizer에 합치는 것이 가능한 것이다.

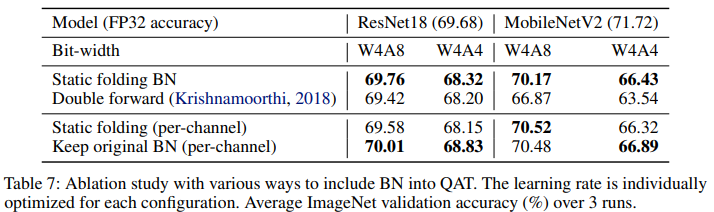
Experiment

위 Table 7을 보면, per-tensor quantization의 경우에 앞서 설명한대로 double forward 방법이 static folding에 비해 성능이 오히려 좋지 않은 것이 확인된다. 반면 per-channel quantization의 경우 static folding을 하는 것보다도 설명한대로 BN을 그냥 두고 inference time에만 quantizer에 합치는 방법이 대체로 더 효과적인 것을 알 수 있다.

4.3. Initialization for QAT

이 장에서는 QAT를 시작할 때 parameter를 어떻게 초기화하는 것이 좋은지를 다룬다. 우선, 시작 시 pretrained된 FP32 모델에서 시작하는 것이 좋다는 것은 이론의 여지가 없다.

논문에 따르면 사전학습된 FP32 모델을 quantize할 때에는 quantization range를 min-max보다는 MSE를 사용해 정하는 것이 초기 학습에는 더 좋다. 그러나 training을 계속 진행하면 둘 사이의 격차는 점점 줄어 큰 차이가 없게 된다고 한다.

또한, plain PTQ에서도 문제가 있었던 모델들(e.g. depth-wise separable convolution을 사용)의 경우 initial parameter를 정할 때에도 Cross-Layer Equalization(CLE)나 bias correction 등의 테크닉을 적용해야만 제대로 훈련이 되는 경우가 발생했다.

4.4. Standard QAT Pipeline

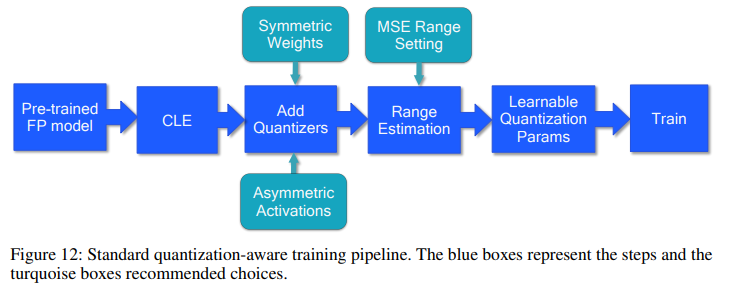
위의 Figure 12는 QAT의 과정을 표준화하여 그림으로 나타낸 것이다.

4.5. Experiments

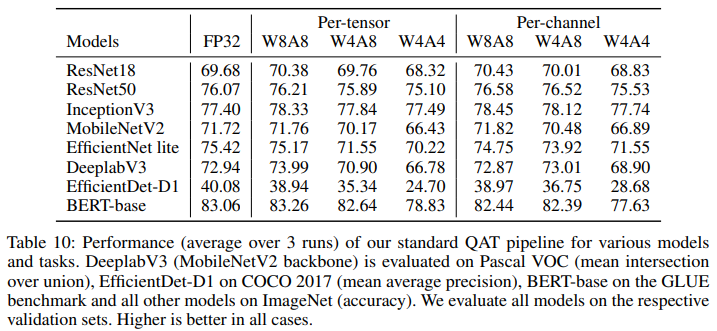
위 Table 10은 4.4에서 제시한 표준적인 QAT 방법론을 적용해 다양한 task에 사용되는 네트워크들을 quantize한 결과물이다. 위의 세 개는 depthwise separable convolution이 없는 것들, 그 아래의 네 개는 있는 것들이며 NLP에 사용되는 BERT-base가 포함되어 있다.

Depthwise convolution이 없는 모델들은 W8A8과 W4A8까지는 FP32 성능과 거의 차이가 없거나 오히려 더 높아지는 결과가 나오기도 했다. 이는 quantized noise가 주입되며 regularizing effect가 작용하였고 추가적인 fine-tuning이 되었기 때문에 나타나는 현상으로 해석될 수 있다. W4A4까지 quantize를 했을 때는 성능이 조금 낮아졌으나 하락폭은 1%정도로 제한적이었다.

반면 depthwise convolution이 있는 모델들은 weight가 4비트로 quantize되었을 때는 성능의 하락이 어느 정도 크게 나타났다. 특히 W4A4에서는 EfficientDet-D1과 같이 성능 저하의 폭이 매우 큰 모델들도 있었다. 다만 Per-channel로 granularity를 변경하면 하락폭이 감소하였다.

BERT-base의 경우, W8A8까지는 성능에 전혀 무리가 없었고 W4A8에서는 1%정도의 성능 저하만이 나타났으며, W4A4에서야 유의미한 성능 저하가 있었다.

5. Summary and Conclusions

뉴럴 네트워크가 생활 속 곳곳에 탑재되어 가는 추세 속에서, NN quantization은 on-device deep learning의 에너지와 latency를 증가시키기 위한 좋은 방법으로 사용될 수 있다.

Quantization을 위한 알고리즘은 크게 두 가지로 나뉠 수 있는데, Post-Training Quantization과 Quantization-Aware Training이다. PTQ의 경우 이미 훈련된 네트워크에 추가적인 데이터나 훈련 없이 즉석에서 quantization이 가능하다. 반면 QAT의 경우 simulated quantization operation을 통해 모델을 low bitwidth에서 다시 훈련시킨다. 이는 시간과 노력은 많이 들지만 더 공격적인 quantization을 가능하게 한다.

사용하고자 하는 애플리케이션의 정확도와 에너지 요구사항에 따라 PTQ와 QAT 사이 적절한 것을 선택하면 될 것이다.