Z. Mo et al., “LUT Tensor Core: A Software-Hardware Co-Design for LUT-Based Low-Bit LLM Inference”, ISCA ‘25
Recently, I was conducting some research on model compression including quantization. This also made me interested in architectural support for this area, and led me to read this paper. The paper "LUT Tensor Core" implements tensor core-like hardware using lookup tables for extreme quantization scenarios such as binary or ternary (1.58-bit) quantization. It was fascinating to see how the HW-SW co-design incorporating lookup tables could be used to implement mixed precision GEMM (mpGEMM) in a highly efficient way.
Introduction
Mixed-precision GEMM (mpGEMM) occurs during quantized inference when activation and weight precisions differ. For example, input activations may be in FP16/INT8 while weights are INT4/2/1. However, in actual computation, hardware dequantizes the values in prior to computation, leading into an inefficiency.
Look-up table(LUT)-based mpGEMM, which is possible in a low-bit regime, has gained a lot of attention recently. That is, all possible combinations of dot product results are pre-computed for a weight row. This is especially effective in extreme quantization scenarios like INT1 (e.g., BitNet).
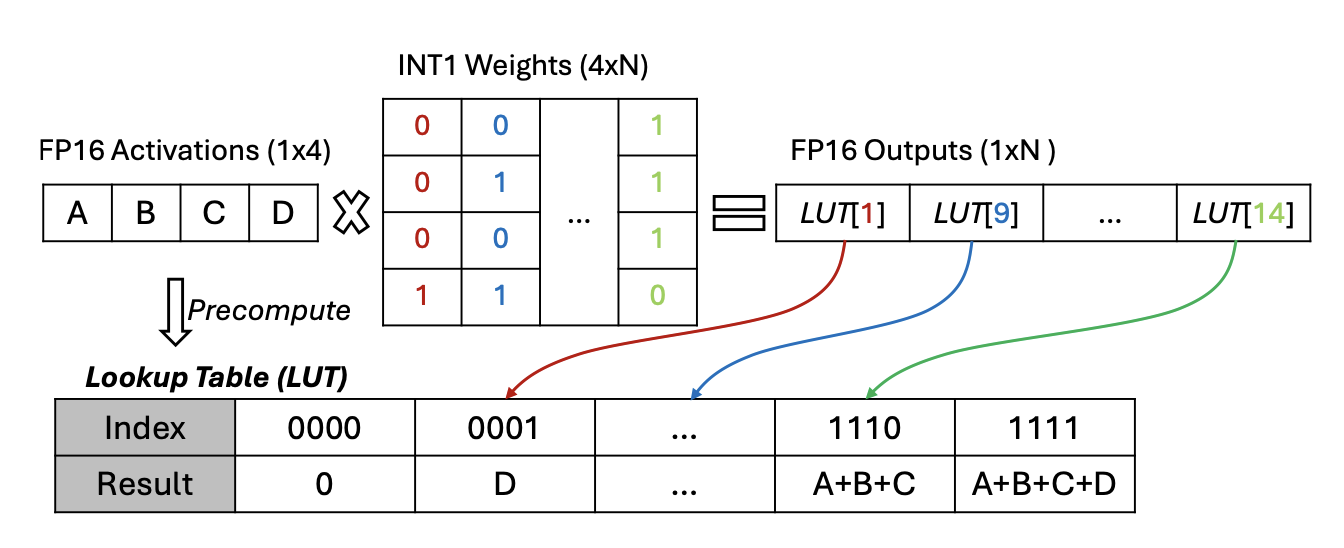
However, the authors point out that LUT-based mpGEMM does not perform well in reality:
- SW issue: Since LUT kernel is not well supported by instructions, its memory access pattern is unoptimized, and thus more inefficient than dequantization-based one.
- HW issue: conventional LUT design lacks optimization since it was not designed with a lot of consideration about mpGEMM. Moreover, storing pre-computation results incurs a lot of overhead.
LUT Tensor Core copes with such problems by conducting a HW-SW co-design: precomputation and storage management, which is a tricky part for hardware, is handled by software. The implementation incorporates three following parts:
-
SW Optimization:
- Precomputation is split by independent operators and then fused to other ones, thereby reducing the number of memory accesses.
- {0, 1} is reinterpreted as {-1, +1} to reduce the table size by half, mitigating storage overhead.
-
HW Customization
- Bit-serial-like circuit to support various combinations of mixed precision.
- Design space exploration (DSE) to determine the shape of LUT-based tensor core, finding that elongated tiles enable efficient table reuse.
- Extends existing matrix multiply-accumulate (MMA) instruction set to implement LUT-based MMA (LMMA) instruction set.
The authors validated the effectiveness of LUT Tensor core by testing it with Accel-Sim, a GPU simulator.
- power and chip area reduced 4x and 6x, respectively.
- speedup: 1.42x for GEMV, 72.2x for GEMM
Background and Motivation
LLM Inference and Low-Bit Quantization
The authors first discusses the importance of quantization, including PTQ and QAT, specifically mentioning BitNet and ParetoQ. Such low bit-width regime is where the authors' method is optimized for. The authors also mention the difficulties of activation quantization, which arises from their nature, generated on-the-fly with high variance due to outliers.
LUT-Based mpGEMM for Low-Bit LLM
LUT-based mpGEMM breaks down matrix multiplications into smaller tiles and then precomputes all possible outcomes for specific activation values within each tile. This dramatically reduces computational cost by preventing the calculation and storage of values that would be impossible given the tile’s activation values. For comparison, precomputing all possible results of FP16 x INT4 would require $2^{16} \times 2^4$ entries, which is far more expensive.
Gaps in Current LUT-based Solutions
The existing HW/SW implementation is not sufficient to support LUT-based mpGEMM:
LUT Tensor Core Design
SW-Based Table optimization
Naively $(2^\text{W\_BIT})^K$ entries are required if the weight bit width is W\_BIT. LUT Tensor Core addresses such overhead by incorporating an optimization technique similar to bit-serial. Bit-serial decomposes an $W$-bit integer into $W$ INT1's, performing the multiplication on them via bit shifts. This reduces the table size into $2^K$, but causes a significant HW overhead. LUT Tensor Core improves upon this with four optimizations: (1) dataflow graph transformation, (2) operator fusion, (3) weight reinterpretation, and (4) table quantization.
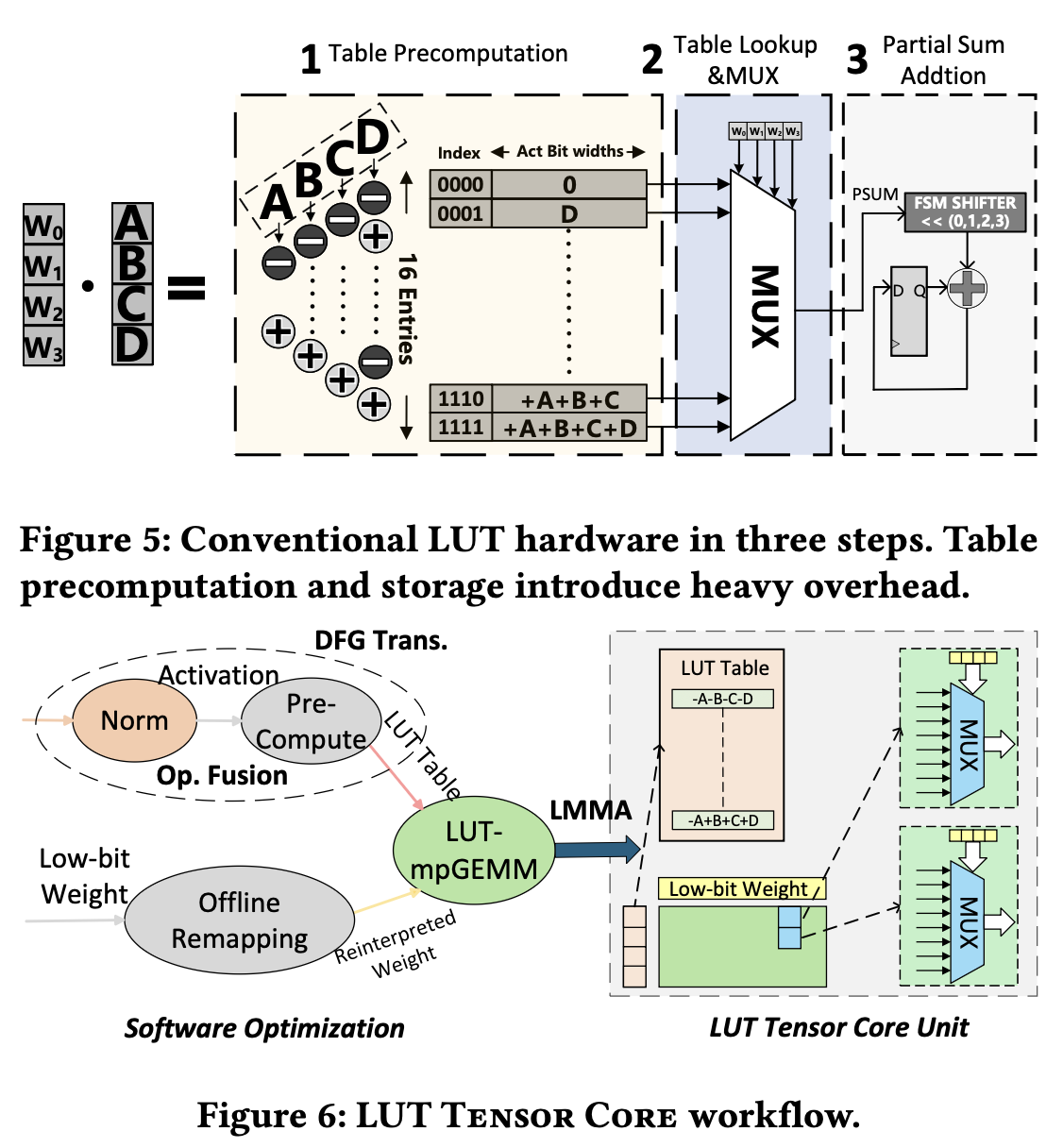
- In the existing LUT implementations, precompute unit adjacent to the table performs the computation on-the-fly.
- However, this requires multiple precompute units for the operation, which causes redundant HW cost.
- To address this, the authors transformed the data flow graph (DFG) so that precomputation is held in a different kernel. This enables all LUT units to use a single precomputation result, reducing the overhead by over 100x.
- To reduce memory traffic from broadcasting, the precompute operator is fused with the preceding operator. Fig. 6 above shows fusion with Norm operator.
Reinterpreting weight for table symmetrization
Original quantized weight $q_w$ is unsigned int, expressing actual values as:
$$r_w = s_w(q_w - z_w)$$
By transforming to $$q'_w = 2q_w - (2^K - 1), \quad s'_w = s_w/2, \quad z'_w = 2z_w + 1 - 2^K$$,
$r_w =s_w^{\prime}(q_w^{\prime}-z_w^{\prime})$ remains unchanged while $q_w^\prime$ now becomes symmetric around 0 (symmetrization).
With this representation, the dot product with activation becomes: $$DP = \sum Act_i s_w(q_{wi} - z_w) = \sum Act_i s'_w (q'_{wi} - z'_w)$$. Through symmetrization, it holds that
$$\text{LUT}[W_3 W_2 W_1 W_0] = \begin{cases} -\text{LUT}[\sim (W_2 W_1 W_0)], & \text{if } W_3 = 1 \ \text{LUT}[W_2 W_1 W_0], & \text{if } W_3 = 0 \end{cases}$$, reducing the number of table entries by half ($2^K \rightarrow 2^{K-1}$).
Table quantization
LUT Tensor Core quantizes the precomputed table itself in a lower precision (e.g., INT8), in case of high activation precision such as FP16/32. By keeping the group size small, such as 4, high precision is maintained while simplifying HW.
LUT-based Tensor Core Microarchitecture
Simplified LUT unit design with bit-serial
As discussed above, a bit-serial circuit architecture is introduced to support various combinations of precisions. That is, weight bit width is mapped to W_BIT cycles so that a bit width greater than 1 is processed serially.
Elongated LUT tiling
Akin to previous tensor cores processing matmul in a tiled manner, LUT Tensor core needs to select tile dimensions.
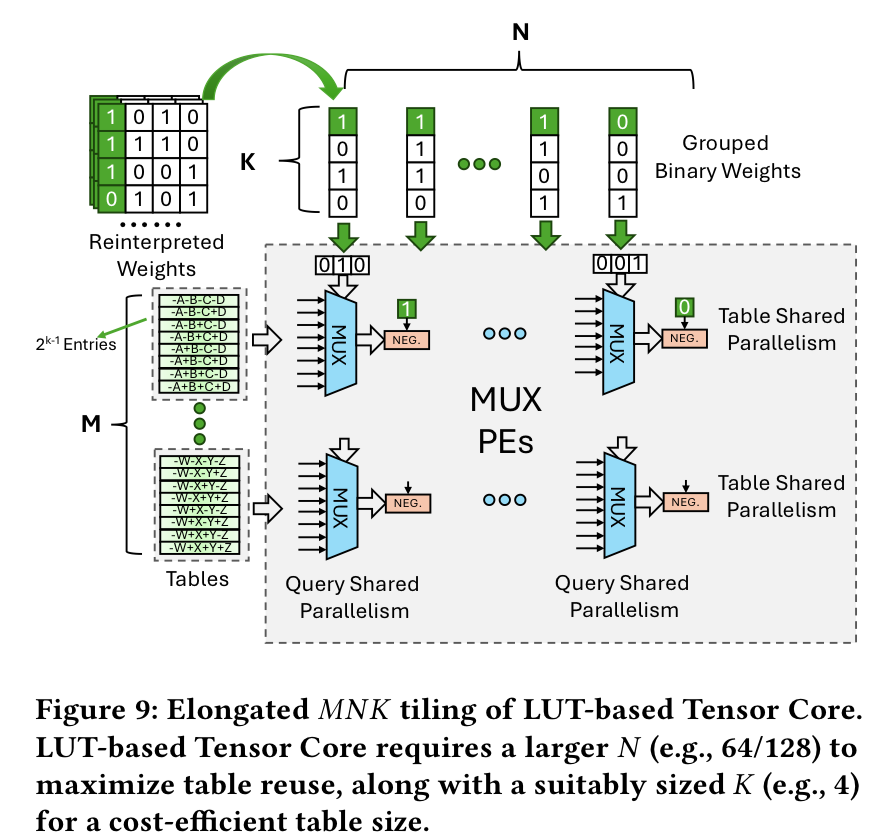
Consider an $MNK$ tile with $M$ tables, $N$ weight sets, and $K$ weights per set.
- Weight tile is $M\times N$, while activation tile is $N\times K$. This requires $M \times N$ mux units.
- total table size = $M\times 2^{K-1}\times \text{LUT\_BIT}$ ($\because$ each table consists of $2^{K-1}$ entries)
- grouped binary weight size: $K\times N \times \text{W\_BIT}$
This makes elongated tile shapes to be advantageous, since:
- Large $K$ causes exponential increase in table entries, which is undesirable
- Large $N$ allows MUX units to reuse table entries extensively, which is beneficial
Instruction and Compilation
LUT-based MMA instructions
The existing GPU architecture is extended to integrate LUT Tensor Core. Specifically, the following instruction set is created:
lmma.{M}{N}{K}.{$A_\text{dtype}$}{$W_\text{dtype}$}{$Accum_\text{dtype}$}{$O_\text{dtype}$}
- Here, {A, W, Accum, O}_dtype represent the data types of activation, weight, accumulation, and output tensors, respectively
- Each warp computes $O_{dtype}[M, N] = A_{dtype}[M, K] \times W_{dtype}[N, K] + Accum_{dtype}[M, N]$
Compilation support and optimizations
End-to-end LLM compilation is implemented using TVM, Roller, and Welder to automatically generate kernels that utilize LUT-based Tensor Core.
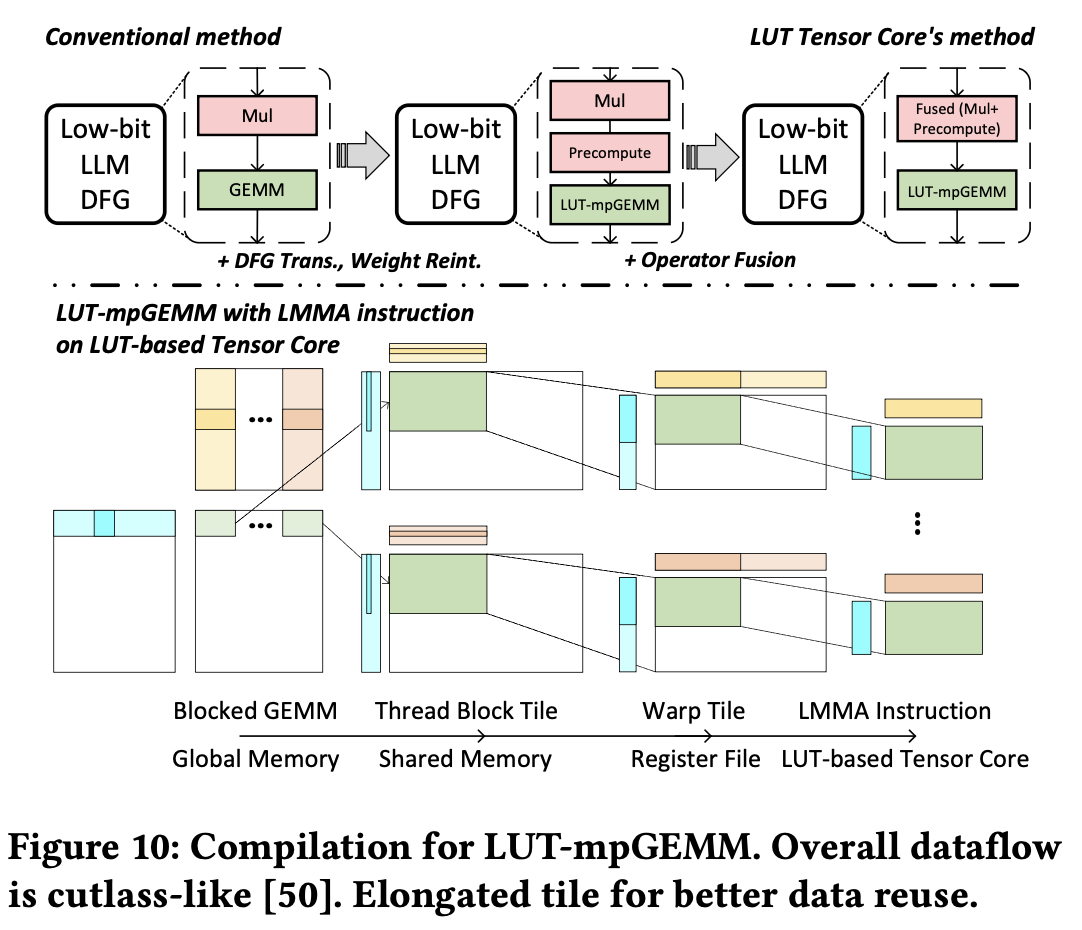
The compilation process can be summarized as follows:
- DFG Transformation: Given a model represented by DFG, an mpGEMM operator is decomposed to precompute operator + LUT-mpGEMM operator. The transformed graph is passed to Welder's graph optimization.
- Operation Fusion: Welder is utilized to fuse the precompute operator with the preceding element-wise operator.
- LUT-mpGEMM Scheduling: a tiling strategy is determined, considering the memory hierarchy. Since LUT-mpGEMM has inputs with data type different to each other, tiling is registered with data sizes rather than shapes. This is registered to the rTile interface of Roller, which finds the optimal configuration.
- Code Generation: Once the final scheduling plan is determined, TVM is used for code generation.. LMMA instructions are registered as TVM intrinsics, allowing TVM to generate kernel codes incorporating LMMA instructions according to the scheduling plan.
Evaluation
- Hardware PPA (Power, Performance Area) measurement: Using Synopsys design compiler and TSMC 28nm process, achieved compute density of 61.55 TFLOPS/mm², approximately 18× higher than the MAC-based implementation's 3.39 TFLOPS/mm²
- Accel-Sim GPU Simulator kernel evaluation: End-to-end evaluation of actual LLM models including LLAMA, OPT, and BLOOM, achieving up to 8.2× inference speedup
- Comparison with SOTA LUT kernel: Speedup of 1.42× for GEMV and 72.2× for GEMM
Z. Mo et al., “LUT Tensor Core: A Software-Hardware Co-Design for LUT-Based Low-Bit LLM Inference”, ISCA ‘25
Quantization을 포함한 모델 경량화 연구에 관심을 가지고 연구를 진행하던 중, 이를 위한 architectural support에 대한 연구에도 흥미가 생겨 읽게 된 논문이다. Weight quantization, 특히 INT1 등 extreme quantization이 이뤄진 경우 lookup table을 이용해 tensor core-like HW를 매우 효율적으로 구현할 수 있었다는 점에서 아주 흥미롭게 읽었다.
Introduction
Quantized inference시 필연적으로 activation과 weight의 정밀도가 다른 mixed-precision GEMM (mpGEMM)이 발생
- input activation은 FP16/INT8 등인데 weight는 INT4/2/1
- 그러나 많은 경우 실제 하드웨어에서는 dequantize 후 계산 → 비효율적
Low-bit에서는 Look-up Table (LUT) 기반 mpGEMM이 가능함.
- weight row의 가능한 모든 combination에 대해 미리 dot product 결과를 precompute하는 것
- 즉 INT1과 같은 extreme quantization scenario에 매우 유리

- 그러나 실제로는 성능이 좋지 않음
- SW 문제: instruction으로 support되는 것이 아니다보니, LUT kernel은 memory access가 dequantization kernel보다 inefficient.
- HW 문제: conventional LUT design은 mpGEMM을 염두에 두고 만들어진 것이 아니라 최적화가 부족. 또, pre-computation 결과 저장에 많은 overhead가 들어감
→ LUT Tensor Core는 HW-SW co-design을 통해 이러한 문제를 해결.
- HW-unfriendly한 작업인 precomputation/storage management를 SW가 해결
-
SW Optimization:
- precomputation을 여러 개의 independent operator로 쪼갠 후 fuse. 이를 통해 memory access 수를 줄임
- storage overhead를 줄이기 위해서 {0, 1}을 {-1, 1}로 재해석, table 크기를 절반으로 줄임
-
HW Customization
- bit-serial-like circuit을 가지고 있어 여러 조합의 mixed precision을 지원.
- Design space exploration (DSE)을 통해 LUT-based tensor core의 shape을 결정하고, tile을 길게 만들어야 efficient table reuse가 가능하다는 것을 밝힘
-
New Instruction and compilation support
- 기존의 matrix multiply-accumulate (MMA) instruction set을 확장해 LUT-based MMA (LMMA) instruction set을 개발.
GPU HW Simulator인 Accel-Sim으로 이를 테스트해 검증.
- power와 area가 각각 4배, 6배 감소.
- speedup: 1.42x for GEMV, 72.2x for GEMM
Background and Motivation
LLM Inference and Low-Bit Quantization
Deployment에 있어서 quantization(PTQ, QAT)의 중요성을 언급. 특히 BitNet과 ParetoQ를 언급.
- activation은 On-the-fly로, (outlier로 인한) 큰 variance를 가지며 생성되기 때문에 quantization이 어려움 또한 언급함.
LUT-Based mpGEMM for Low-Bit LLM
mpGEMM을 작은 tile의 단위로 나눈 후, tile에 속한 specific한 activation value들로 나올 수 있는 모든 조합을 precompute하는 식.
- FP16 x INT4의 모든 조합을 미리 계산하려면 $2^{16} \times 2^4$개 entry가 필요. 이것보다 훨씬 효율적 (등장하지 않는 FP값에 대해서는 계산하지 않는 것)
Gaps in Current LUT-based Solutions
기존의 HW/SW implementation은 LUT-based mpGEMM을 지원하기에 충분하지 않음
Bit-serial (기존의 optimization 기법)
- W_BIT integer를 W개의 1-bit integer로 분해, 1-bit integer들에 대해 곱셈을 bit shift로 수행
- Table size를 $2^K$로 감소시키지만 상당한 HW overhead를 발생시킴
LUT Tensor Core는 네 가지 최적화로 이를 개선: (1) dataflow graph transformation, (2) operator fusion, (3) weight reinterpretation, (4) table quantization

- 기존 implementation에서는 각 LUT unit마다 옆에 놓인 precompute unit이 on-the-fly로 계산이 이루어지도록 했음
- 그러나 이 경우 동일 operation을 하는 여러 개의 precompute unit 필요 → 불필요한 HW cost
- LUT Tensor Core에서는 이러한 비효율을 극복하기 위해 DFG를 변형해, precomputation은 별도의 kernel에서 수행하도록 함 → 한 번의 precomputation으로 모든 LUT unit이 사용가능하도록
- precomputation overhead를 100x 이상 감소
- broadcasting으로 인한 memory traffic을 줄이기 위해서는 precompute operator를 직전의 operator와 fuse (Fig. 6, 그림에서는 Norm과 fuse됨)
Reinterpreting weight for table symmetrization
원래의 quantized weight $q_w$는 unsigned int로써,
$$r_w = s_w(q_w - z_w)$$
와 같이 실제 값을 표현하게 됨. 이를 $$q'_w = 2q_w - (2^K - 1), \quad s'_w = s_w/2, \quad z'_w = 2z_w + 1 - 2^K$$와 같이 변형시 $r_w =s_w^{\prime}(q_w^{\prime}-z_w^{\prime})$이 유지되면서도 $q_w^\prime$은 0 주위로 symmetric한 값을 가지게 됨 (symmetrization)
이렇게 나타내면 activation과의 dot product는 $$DP = \sum Act_i s_w(q_{wi} - z_w) = \sum Act_i s'_w (q'_{wi} - z'_w)$$로 표현. 이렇게 symmetrization을 함으로써,
$$\text{LUT}[W_3 W_2 W_1 W_0] = \begin{cases} -\text{LUT}[\sim (W_2 W_1 W_0)], & \text{if } W_3 = 1 \ \text{LUT}[W_2 W_1 W_0], & \text{if } W_3 = 0 \end{cases}$$
와 같이 table entry의 수를 절반으로 줄일 수 있음 ($2^K \rightarrow 2^{K-1}$).
Table quantization
activation의 정밀도가 FP16/32와 같이 높은 경우에는 위와 같이 precompute된 table 자체를 다시 INT8등 낮은 정밀도로 quantize함.
- group size는 4 정도로 낮게 설정 → 높은 정밀도를 유지하면서도 HW를 단순화
LUT-based Tensor Core Microarchitecture
Simplified LUT unit design with bit-serial
Weight에서 flexible한 bit-width를 지원하기 위해 bit-serial circuit architecture를 도입
- weight bit width를 W_BIT개의 cycle에 매핑해서 1 초과의 bit width는 serial하게 처리하도록 함
Elongated LUT tiling
기존 Tensor core가 tiling으로 행렬곱을 처리하는 것처럼, LUT Tensor core에서도 tiling dimension을 선택해야.

- $M$개 table, $N$개의 weight set, set당 weight의 개수 $K$인 $MNK$ tile을 고려
- weight tile이 $M\times N$, activation tile이 $N\times K$
- floating point set이 $K$개라고 생각하면 됨
- Mux unit이 $M\times N$개
- total table size = $M\times 2^{K-1}\times \text{LUT\_BIT}$ ($\because$ 각 table은 $2^{K-1}$개 entry로 구성되므로 )
- grouped binary weight size: $K\times N \times \text{W\_BIT}$
- Tile shape이 길쭉할수록 유리함 (elongated LUT tiling)
- $K$가 커지면 table entry 개수가 지수적으로 증가하니 안됨
- $N$이 커지면 MUX unit이 table entry를 많이 재사용할 수 있게 되어 좋음
Instruction and Compilation
LUT-based MMA instructions
기존의 GPU architecture를 확장해 LUT Tensor Core를 통합시킴. 구체적으로는 다음과 같은 instruction set을 만듦:
lmma.{M}{N}{K}.{$A_\text{dtype}$}{$W_\text{dtype}$}{$Accum_\text{dtype}$}{$O_\text{dtype}$}
- 여기에서 {A, W, Accum, O}_dtype은 각각 activation, weight, accumulation, output tensor의 type
- 각 warp는 $O_{dtype}[M, N] = A_{dtype}[M, K] \times W_{dtype}[N, K] + Accum_{dtype}[M, N]$를 계산하게 됨.
Compilation support and optimizations
LUT-based Tensor Core를 활용한 kernel을 자동으로 생성하도록 TVM, Roller, Welder를 활용해 end-to-end LLM compilation을 구현

Compilation 과정
- DFG Transformation: DFG로 표현된 model representation이 주어지면 mpGEMM operator를 precompute operator + LUT-mpGEMM operator로 바꿈. 이렇게 변환된 결과는 Welder의 graph optimization에 pass.
- Operation Fusion: Welder를 사용해 precompute operator를 직전의 element-wise operator와 fuse함
- LUT-mpGEMM Scheduling: memory hierarchy를 고려해 tiling 전략을 결정. 이때 기존의 방식과는 달리 LUT-mpGEMM은 입력들이 서로 다른 data type을 가지기 때문에, tiling을 shape이 아닌 memory size로 표현하여 등록함. 이를 Roller의 rTile interface에 등록해 optimal configuration을 찾음
- Code Generation: 최종 scheduling 계획이 확정되면 TVM을 사용하여 코드 생성. 이때 LMMA 명령어를 TVM의 intrinsic으로 등록하면 TVM이 scheduling 계획에 따라서 LMMA 명령어가 포함�kernel 코드를 작성
Evaluation
- Hardware PPA (Power, Performance Area) 측정: Synopsys design compiler, TSMC 28nm 공정을 사용해 61.55 TFLOPS/mm${}^2$의 compute density를 달성함. 이는 3.39 TFLOPS/mm${}^2$를 달성한 MAC-based implementation보다 약 18배 높은 결과.
- Accel-Sim GPU Simulator를 이용한 kernel evaluation: end-to-end로 LLAMA, OPT, BLOOM 등 실제 LLM 모델을 평가, 최대 8.2배의 inference speedup 달성.
- SOTA LUT kernel과의 비교: GEMV에서 1.42배, GEMM에서 72.2배에 달하는 speedup.