Optimizing CUDA Matrix Multiplication: From Tiling to Tensor Cores

Dec. 23, 2024, 12:26 a.m. ยท 7 min read ยท ๐ŸŒ๏ธŽ en/ko

CUDA GPU

During this semester's Scalable High-Performance Computing course, I worked on optimizing matrix multiplication using various libraries and APIs including pthread, OpenMP, OpenCL, CUDA. Also, in the final project, I was able to gain valuable experience accelerating deep learning model inference using a cluster of GPU nodes, contemplating various ideas to accelerate different kernels and applying optimization techniques. Even in the final project, optimizing the matrix multiplication (matmul) kernel was the crucial part where I put most of my time and endeavors.

In this article, I aim to summarize optimization techniques applied to CUDA implementation step-by-step, starting from a naive approach. By incrementally applying each optimization, I will document how much each technique improves performance. Note that the performance measurements were all conducted with $A\in \mathbb{R}^{M\times K}, B \in \mathbb{R}^{K \times N}, C \in \mathbb{R}^{M\times N}, M=N=K=4096$ on an NVIDIA GeForce RTX 3060. All codes can be found at https://github.com/vantaa89/cuda-matmul/tree/master.

Kernel 0: Naive Matrix Multiplication

__global__ void matmul_kernel_naive(float *A, float *B, float *C, int M, int N, int K) {
  int row = threadIdx.x + blockDim.x * blockIdx.x;
  int col = threadIdx.y + blockDim.y * blockIdx.y;
  float acc = 0;
  for(int k = 0; k < K; ++k){
    acc += A[row * K + k] * B[k * N + col];
  }
  C[row * N + col] = acc;
}

// Host code for launch
dim3 blockDim(32, 32);
dim3 gridDim((M+31)/32, (N+31)/32);
matmul_kernel_naive<<<gridDim, blockDim>>>(a_d, b_d, c_d, M, N, K);

This is the most basic matrix multiplication kernel. It uses a grid with M rows and N columns, where the $(i, j)$-th thread calculates $C_{ij}$. However, it doesn't use shared memory, repeatedly fetching matrices A and B directly from global memory. The memory access pattern has not been optimized yet. A throughput of 103 GFLOPS was measured.

Kernel 1: Block Tiling

template <int BLOCK_SIZE>
__global__ void matmul_kernel_block_tiling(float *A, float *B, float *C, int M, int N, int K) {
  int row = threadIdx.x;
  int col = threadIdx.y;
  int global_row = BLOCK_SIZE * blockIdx.x + threadIdx.x;
  int global_col = BLOCK_SIZE * blockIdx.y + threadIdx.y;
  __shared__ float A_block[BLOCK_SIZE][BLOCK_SIZE];
  __shared__ float B_block[BLOCK_SIZE][BLOCK_SIZE];
  float acc = 0.0f;
  const int num_tiles = (K + BLOCK_SIZE - 1) / BLOCK_SIZE;

  for(int t = 0; t < num_tiles; ++t){
    const int tiled_row = BLOCK_SIZE * t + row;
    const int tiled_col = BLOCK_SIZE * t + col;    
    A_block[row][col] = A[global_row * K + tiled_col];            
    B_block[row][col] = B[tiled_row * N + global_col];
    __syncthreads();
    for(int k = 0; k < BLOCK_SIZE; ++k){
      acc += A_block[row][k] * B_block[k][col];
    }   
    __syncthreads();
  }
  C[global_row * N + global_col] = acc;
}

// Host code for launch
const int BLOCK_SIZE = 16;
blockDim = dim3(BLOCK_SIZE, BLOCK_SIZE);
gridDim = dim3((M+BLOCK_SIZE-1)/BLOCK_SIZE, (N+BLOCK_SIZE-1)/BLOCK_SIZE);
matmul_kernel_block_tiling<BLOCK_SIZE><<<gridDim, blockDim>>>(a_d, b_d, c_d, M, N, K);

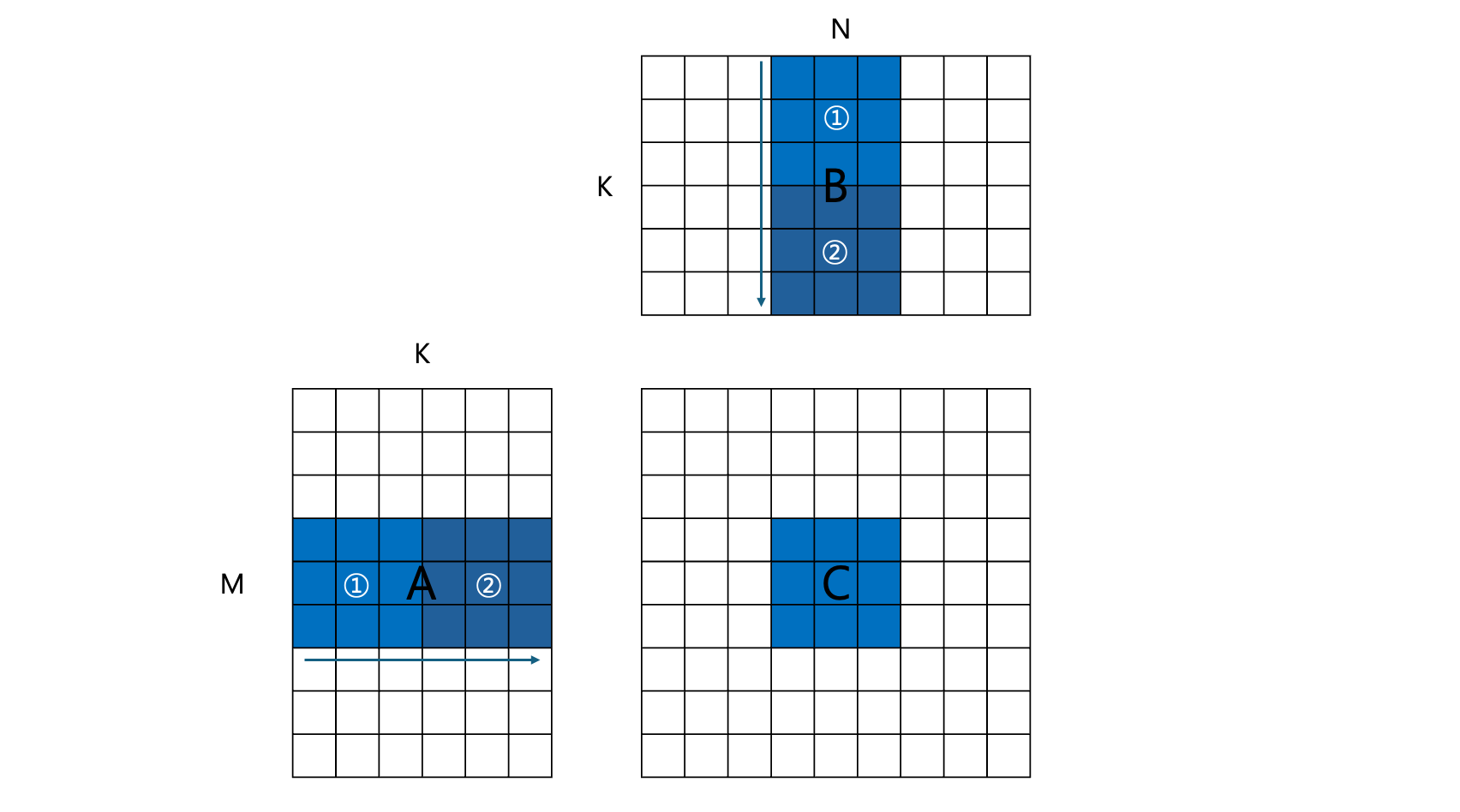
This is the kernel where a basic optimization called tiling is applied. In particular, the number of global memory accesses was significantly reduced by employing shared memory. Since each of the thread blocks processes a single tile of the resultant matrix $C$, this can be dubbed as block tiling. The figure above represents a thread block that computes the $3\times 3$ sub-matrix of $C$, colored in blue.

As demonstrated in the code, a thread block comprises BLOCK_SIZE * BLOCK_SIZE($16\times 16$) threads. In the figure, this is reduced to $3\times 3$ for convenience, meaning there are $3\times 3$ different threads in a thread block.

First, the thread block reads the elements of $A$ and $B$ belonging to โ‘  from global memory, and copies them to A<mathsubscript>block and B<mathsubscript>block, which are stored in shared memory. Since there are $3\times 3$ elements to copy from each $A$ and $B$, and the thread block also comprises $3\times 3$ threads, each thread needs to read one element from $A$ and one from $B$.

After the elements are copied to shared memory, the computation is performed for these elements and the results are accumulated to the buffer acc of each thread. The same process is repeated for each โ‘ก, โ‘ข, and so on, by the for-loop over t. Here, __syncthreads() is employed to guarantee that the computation is held after the loading to shared memory is done. The throughput was measured to be 411 GFLOPS.

Kernel 2: Thread Tiling

template <int BLOCK_SIZE, int THREAD_TILE_SIZE>
__global__ void matmul_kernel_thread_tiling(float *A, float *B, float *C, int M, int N, int K) {
  int row = threadIdx.x * THREAD_TILE_SIZE; 
  int col = threadIdx.y;
  int global_row = BLOCK_SIZE * blockIdx.x + row;
  int global_col = BLOCK_SIZE * blockIdx.y + col;
  __shared__ float A_block[BLOCK_SIZE][BLOCK_SIZE];
  __shared__ float B_block[BLOCK_SIZE][BLOCK_SIZE];
  float acc[THREAD_TILE_SIZE];
  for (int wm=0; wm<THREAD_TILE_SIZE; wm++) {
    acc[wm] = 0.0f;
  }

  const int num_tiles = (K + BLOCK_SIZE - 1) / BLOCK_SIZE;

  for(int t = 0; t < num_tiles; ++t){
    const int tiled_row = BLOCK_SIZE * t + row;
    const int tiled_col = BLOCK_SIZE * t + col;
    for(int w1 = 0; w1 < THREAD_TILE_SIZE; w1++){
      A_block[row+w1][col] = A[(global_row+w1) * K + tiled_col];            
      B_block[row+w1][col] = B[(tiled_row+w1) * N + global_col];
    }
    __syncthreads();

    for(int k = 0; k < BLOCK_SIZE; ++k){
      for(int w1 = 0; w1 < THREAD_TILE_SIZE; w1++){
        acc[w1] += A_block[row+w1][k] * B_block[k][col];
      }
    }

    __syncthreads();
  }
  for(int w1 = 0; w1 < THREAD_TILE_SIZE; w1++){
    C[(global_row+w1) * N + global_col] = acc[w1];
  }
}

// Host code for launch
const int BLOCK_SIZE = 32, THREAD_TILE_SIZE = 8;
blockDim = dim3(BLOCK_SIZE/THREAD_TILE_SIZE, BLOCK_SIZE);
gridDim = dim3((M+BLOCK_SIZE-1)/BLOCK_SIZE, (N+BLOCK_SIZE-1)/BLOCK_SIZE);
matmul_kernel_thread_tiling<BLOCK_SIZE, THREAD_TILE_SIZE><<<gridDim, blockDim>>>(a_d, b_d, c_d, M, N, K);

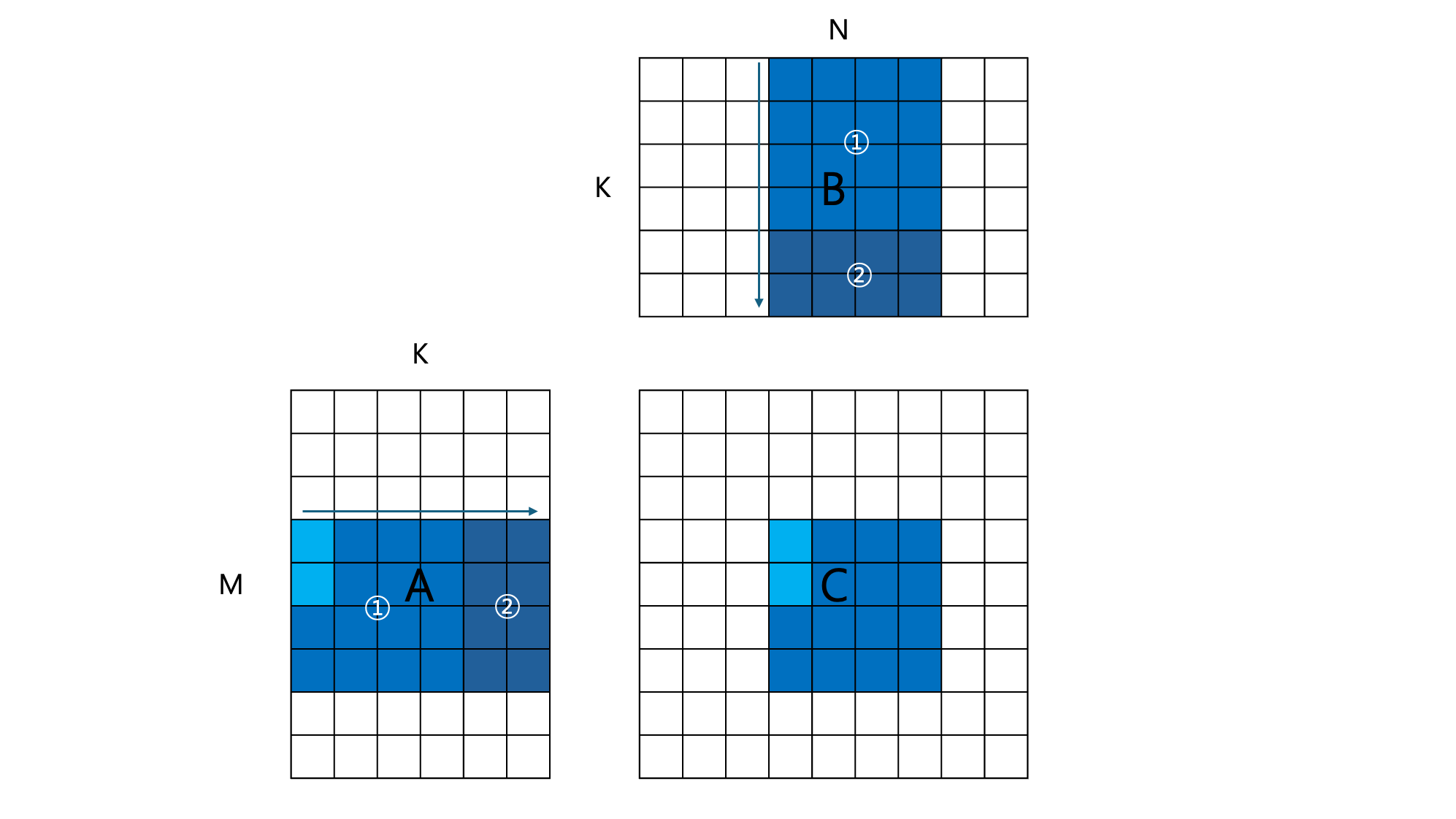
This is very similar to kernel 1, where block tiling is applied. However, while a thread in kernel 1 calculates a single resultant element of $C$, each thread in kernel 2 computes THREAD_TILE_SIZE adjacent elements in the row direction of C. This increases the workload per thread, effectively reducing the overhead which are irrelevant to actual computation.

The figure above shows an example for BLOCK_SIZE=4, THREAD_TILE_SIZE=2. The currently executed thread block is computing the $4\times 4$ sub-matrix of $C$, colored blue. However, since two elements are computed per thread, the thread block size becomes (4, 2), not (4, 4).

One can notice that acc has changed into an array, as opposed to a scalar in the original code. This is because each thread needs multiple accumulators corresponding to each elements of $C$ it is in charge of. Also, since the number of threads within a thread block no longer matches the number of elements in $A$ and $B$ it accesses, we now need a for-loop to load input elements into shared memory (A_block and B_block).

As a result, throughput increases to 745 GFLOPS.

Kernel 3: 2D Thread Tiling

template <int BLOCK_SIZE, int THREAD_TILE_SIZE>
__global__ void matmul_kernel_2d_thread_tiling(float *A, float *B, float *C, int M, int N, int K) {
  int row = threadIdx.x * THREAD_TILE_SIZE;
  int col = threadIdx.y * THREAD_TILE_SIZE;
  int global_row = BLOCK_SIZE * blockIdx.x + row;
  int global_col = BLOCK_SIZE * blockIdx.y + col;
  __shared__ float A_block[BLOCK_SIZE][BLOCK_SIZE];
  __shared__ float B_block[BLOCK_SIZE][BLOCK_SIZE];
  float acc[THREAD_TILE_SIZE][THREAD_TILE_SIZE];
  for (int wm=0; wm<THREAD_TILE_SIZE; wm++) {
    for (int wn=0; wn<THREAD_TILE_SIZE; wn++) {
      acc[wm][wn] = 0.0f;
    }
  }

  const int num_tiles = (K + BLOCK_SIZE - 1) / BLOCK_SIZE;

  for(int t = 0; t < num_tiles; ++t){
    const int tiled_row = BLOCK_SIZE * t + row;
    const int tiled_col = BLOCK_SIZE * t + col;
    for(int w1 = 0; w1 < THREAD_TILE_SIZE; w1++){
      for(int w2 = 0; w2 < THREAD_TILE_SIZE; w2++){
        A_block[row+w1][col+w2] = A[(global_row+w1) * K + tiled_col + w2];            
        B_block[row+w1][col+w2] = B[(tiled_row+w1) * N + global_col + w2];
      }
    }
    __syncthreads();

    for(int k = 0; k < BLOCK_SIZE; ++k){
      for(int w2 = 0; w2 < THREAD_TILE_SIZE; w2++){
        for(int w1 = 0; w1 < THREAD_TILE_SIZE; w1++){
          acc[w1][w2] += A_block[row+w1][k] * B_block[k][col+w2];
        }
      }
    }

    __syncthreads();
  }
  for(int w1 = 0; w1 < THREAD_TILE_SIZE; w1++){
    for(int w2 = 0; w2 < THREAD_TILE_SIZE; w2++){
      if(global_col+w2 < N && global_row + w1 < M)
        C[(global_row+w1) * N + global_col+w2] = acc[w1][w2];
    }
  } 
}

// Host code for launch
const int BLOCK_SIZE = 64, THREAD_TILE_SIZE = 8;
blockDim = dim3(BLOCK_SIZE/THREAD_TILE_SIZE, BLOCK_SIZE/THREAD_TILE_SIZE);
gridDim = dim3((M+BLOCK_SIZE-1)/BLOCK_SIZE, (N+BLOCK_SIZE-1)/BLOCK_SIZE);
matmul_kernel_2d_thread_tiling<BLOCK_SIZE, THREAD_TILE_SIZE><<<gridDim, blockDim>>>(a_d, b_d, c_d, M, N, K);

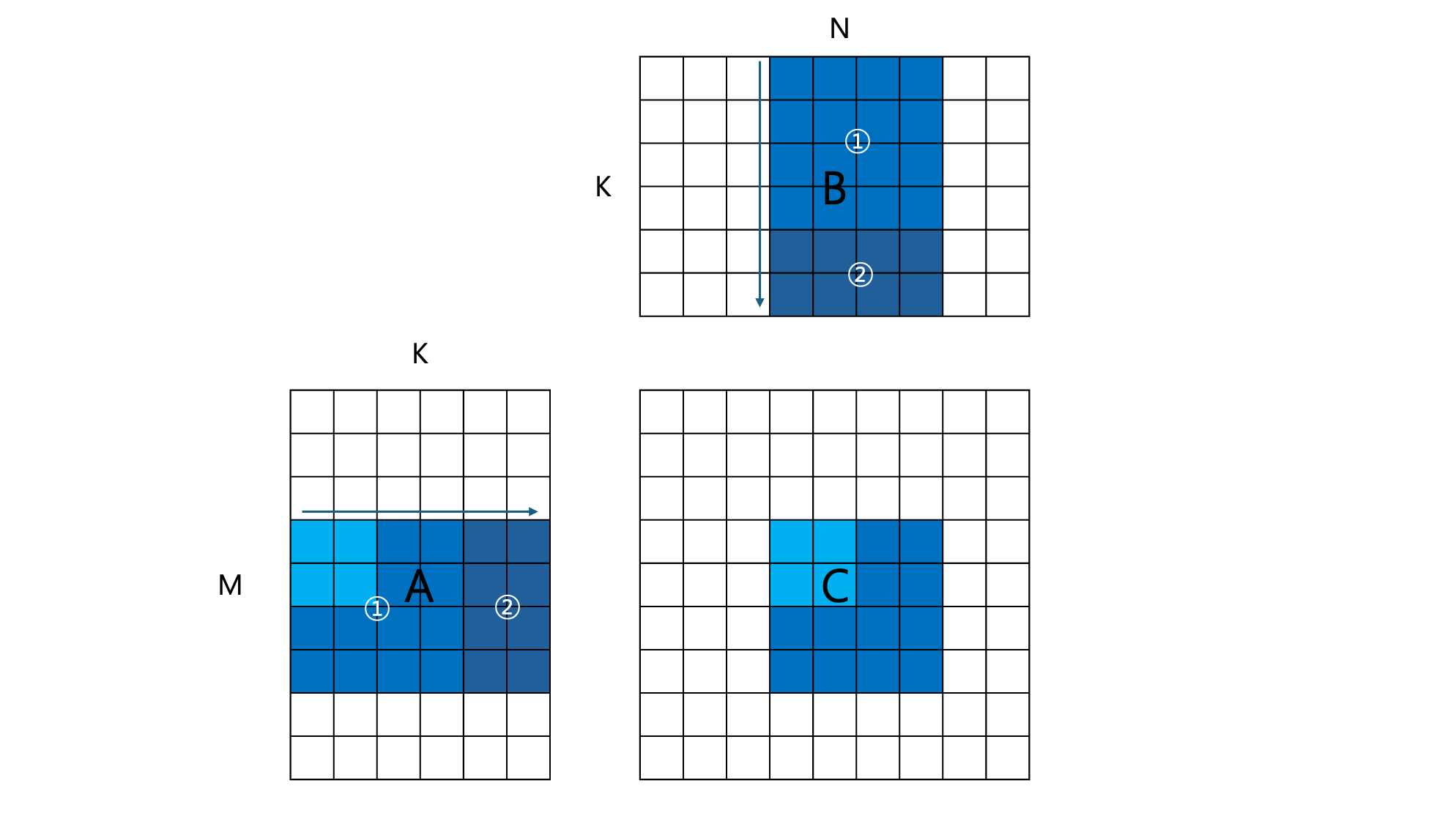
In the previous kernel 2, we improved the performance by increasing the number of elements in $C$ each thread computes. To further optimize the kernel, we can apply such thread tiling in a two-dimensional way. As depicted in the figure above, each thread block computes a sub-matrix of $C$, the resultant matrix, not a single row as it did in kernel 2. This further improved the throughput to 2150 GFLOPS!

Kernel 4: Tensor Core

#define WMMA_SIZE 16

__global__ void matmul_tc(half *A, half *B, float *C, int M, int N, int K){
  int global_row = blockIdx.x * WMMA_SIZE;
  int global_col = blockIdx.y * WMMA_SIZE;

  wmma::fragment<wmma::matrix_a, WMMA_SIZE, WMMA_SIZE, WMMA_SIZE, half, wmma::row_major> a_frag;
  wmma::fragment<wmma::matrix_b, WMMA_SIZE, WMMA_SIZE, WMMA_SIZE, half, wmma::row_major> b_frag;
  wmma::fragment<wmma::accumulator, WMMA_SIZE, WMMA_SIZE, WMMA_SIZE, float> c_frag;
  wmma::fill_fragment(c_frag, 0.0f);

  const int num_tiles = (K + WMMA_SIZE - 1) / WMMA_SIZE;

  for(int t = 0; t < num_tiles; ++t){
    int tiled_col = t * WMMA_SIZE, tiled_row = t * WMMA_SIZE;
    wmma::load_matrix_sync(a_frag, &A[global_row * K + tiled_col], K);
    wmma::load_matrix_sync(b_frag, &B[tiled_row * N + global_col], N); 
    wmma::mma_sync(c_frag, a_frag, b_frag, c_frag);
  }
  wmma::store_matrix_sync(&C[global_row * N + global_col], c_frag, N, wmma::mem_row_major);
}

// Host code for launch
blockDim = dim3(32, 1);
gridDim = dim3((N+WMMA_SIZE-1)/WMMA_SIZE, (M+WMMA_SIZE-1)/WMMA_SIZE);
matmul_tc<<<gridDim, blockDim>>>(a_d, b_d, c_d, M, N, K);

Now tensor cores come into play. Kernel 4 and 5 uses tensor cores to perform matrix multiplication for half-precision (FP16) inputs. Tensor cores are specialized computational units that exist separately from CUDA cores in each streaming multiprocessor of the GPU, allowing threads within a warp to cooperatively perform fast multiplication between two $16\times 16$ matrices. However, tensor cores only accept inputs with reduced precisions, such as FP16, BF16, or even sub-8 bit data types. The output (matrix C) can be chosen as full-precision, but some loss of precision must be considered.

I used a library called WMMA(Warp Matrix Multiply-Accumulate) to utilize tensor core, partly because CUTLASS was not allowed for the project. The basic principles are similar to block tiling (kernel 1), but blockDim must be set to (32, 1) so that a thread block fits exactly in a single warp. Thus, a thread block(=warp) processes a $16\times 16$ submatrix of the resultant matrix $C$.

WMMA operates by performing multiplication between wmma::matrix_a (left matrix) and wmma::matrix_b (right matrix) and accumulating the result in wmma::accumulator. Therefore, wmma::fragment was employed to define the input and output matrices recognized by the tensor core. The buffers defined so are actually distributed and stored in each thread's registers. Then, similar to kernel 1, tiles are slid while accumulating the resultant submatrix. wmma::load_matrix_sync loads 16\times 16 data from global memory into wmma::fragment, wmma::mma_sync performs the actual matrix multiply-accumulate on the loaded values, and wmma::store_matrix_sync writes the data in c_frag to the global memory location. Using tensor cores, the throughput increased to 3066 GFLOPS.

Kernel 5: Tensor Core + Warp Tiling

template<int WARP_TILE_SIZE1, int WARP_TILE_SIZE2>
__global__ void matmul_tc_2d_warp_tiling(half *A, half *B, float *C, int M, int N, int K) {
  int global_row = blockIdx.x * WMMA_SIZE * WARP_TILE_SIZE1; // 0 ~ M
  int global_col = blockIdx.y * WMMA_SIZE * WARP_TILE_SIZE2; // 0 ~ N

  wmma::fragment<wmma::matrix_a, WMMA_SIZE, WMMA_SIZE, WMMA_SIZE, half, wmma::row_major> a_frag;
  wmma::fragment<wmma::matrix_b, WMMA_SIZE, WMMA_SIZE, WMMA_SIZE, half, wmma::row_major> b_frag[WARP_TILE_SIZE2];
  wmma::fragment<wmma::accumulator, WMMA_SIZE, WMMA_SIZE, WMMA_SIZE, float> c_frag[WARP_TILE_SIZE1][WARP_TILE_SIZE2];
  for(int i = 0; i < WARP_TILE_SIZE1; i++){
    for(int j = 0; j < WARP_TILE_SIZE2; j++)
      wmma::fill_fragment(c_frag[i][j], 0.0f);
  }

  const int num_tiles = (K + WMMA_SIZE - 1) / WMMA_SIZE;

  for(int t = 0; t < num_tiles; ++t){
    int tiled_col = t * WMMA_SIZE, tiled_row = t * WMMA_SIZE;
    for(int j = 0; j < WARP_TILE_SIZE2; j++)
      wmma::load_matrix_sync(b_frag[j], &B[tiled_row * N + global_col + j * WMMA_SIZE], N); 

    for(int i = 0; i < WARP_TILE_SIZE1; i++){
      wmma::load_matrix_sync(a_frag, &A[(global_row + i * WMMA_SIZE) * K + tiled_col], K);
      for(int j = 0; j < WARP_TILE_SIZE2; j++){
        wmma::mma_sync(c_frag[i][j], a_frag, b_frag[j], c_frag[i][j]);
      }
    }
  }

  for(int i = 0; i < WARP_TILE_SIZE1; i++){
    for(int j = 0; j < WARP_TILE_SIZE2; j++){
      wmma::store_matrix_sync(&C[(global_row + i * WMMA_SIZE) * N + global_col + j * WMMA_SIZE], c_frag[i][j], N, wmma::mem_row_major);
    }
  }
}


// Host code for launch
const int WARP_TILE_SIZE1 = 4, WARP_TILE_SIZE2 = 4;
blockDim = dim3(32, 1);
gridDim = dim3((N+WMMA_SIZE-1)/WMMA_SIZE/WARP_TILE_SIZE1, (M+WMMA_SIZE-1)/WMMA_SIZE/WARP_TILE_SIZE2);
matmul_tc_2d_warp_tiling<WARP_TILE_SIZE1, WARP_TILE_SIZE2><<<gridDim

Considering the powerful performance of tensor cores, the throughput increase in kernel 4 does not seem to be significant. Particularly, considering that we have sacrificed precision, a 1.5x improvement is not very satisfactory. This can be attributed to significant overhead caused in areas other than actual WMMA computation.

Therefore, applying 2D tiling similar to what was used in kernel 3 can increase the workload per warp, thereby effectively reducing the non-computational overhead. With this applied, each thread block computes a larger sub-matrix than the previous $16\times 16$. In the code, this was achieved by defining an array of wmma::fragment's and performing multiple computations per single load. Applying this optimization resulted in a final throughput increased to 6688 GFLOPS.

Conclusion

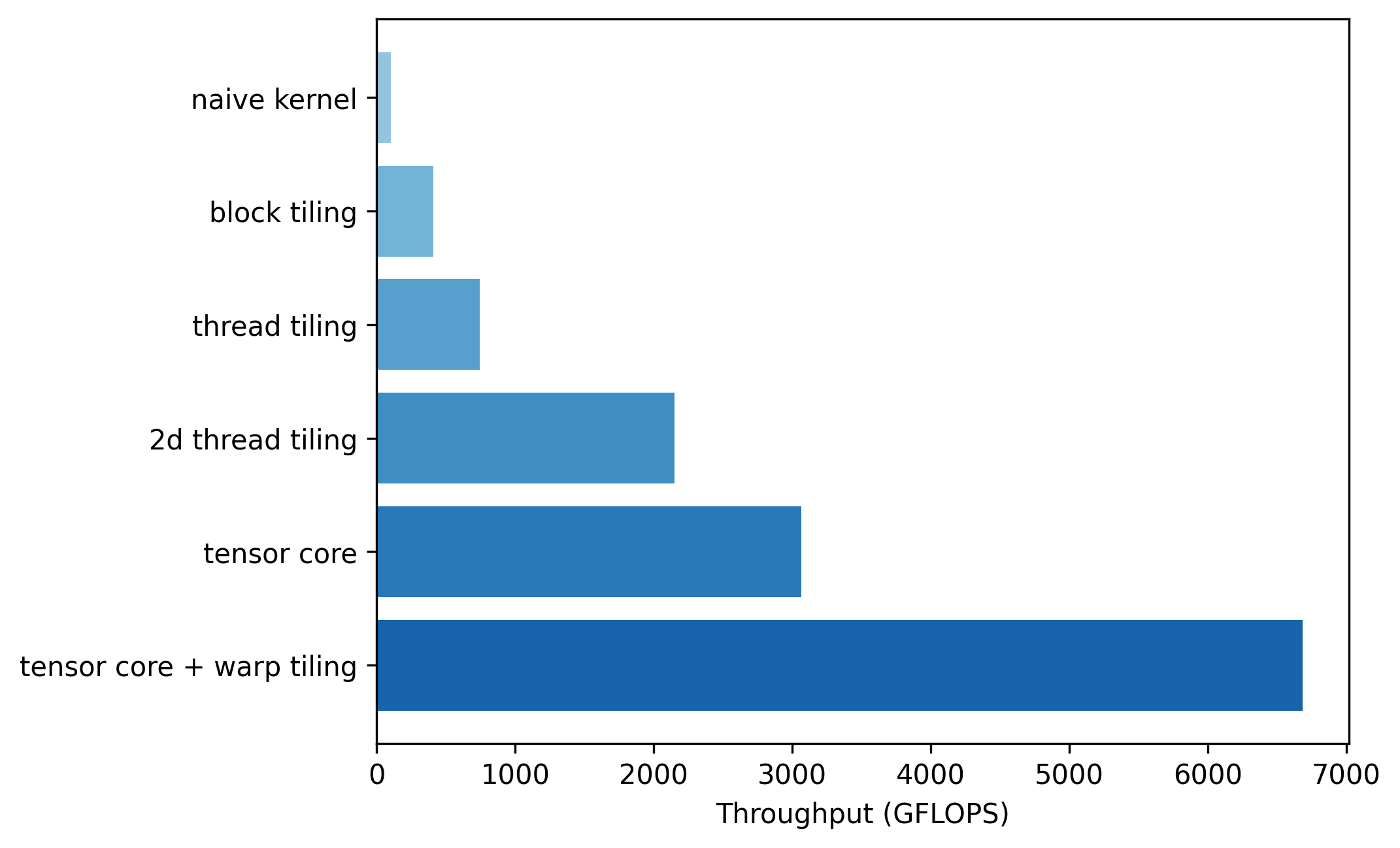
While the naive kernel 0 achieved only 103 GFLOPS, kernel 5 where tensor cores and warp tiling were applied achieved 6688 GFLOPS, showing a 65-fold speedup. Even kernel 3, which didn't sacrifice precision at all, achieved a 21-fold speedup compared to kernel 0, demonstrating how important kernel optimizations are. I also note that I have considered many factors including but not limited to number of global memory I/O accesses, coalesced memory access, and shared memory bank conflicts, while implementing each kernel.

The codes above don't implement boundary checks, so depending on the kernel, they generally produce correct results only when matrix sizes are multiples of 32. Boundary checks can be implemented by writing 0 for out-of-bounds cases when loading values to shared memory, or by using zero padding methods.

References

  1. Otomo Hiroyuki, "Tensorใ‚ณใ‚ขใ‚’ไฝฟใฃใฆใฟใŸ," Fixstars Tech Blog
  2. "OpenCL matrix-multiplication SGEMM tutorial"
  3. Lei Mao, "CUDA Matrix Multiplication Optimization"
  4. Jeremy Appleyard and Scott Yokim, "Programming Tensor Cores in CUDA 9," NVIDIA Technical Blog
  5. Andrew Kerr, Duane Merrill, Julien Demouth and John Tran, "CUTLASS: Fast Linear Algebra in CUDA C++," NVIDIA Technical Blog
Ctrl+K
Start typing to search...